შესავალი
ცოტა ხნის წინ, ახალი კვანტური ეფექტები შესწავლილი იქნა თხელ ნანომესრულ ფენებში. ნანომესრული ზედაპირი ადებს დამატებით სასაზღვრო პირობებს ელექტრონის ტალღურ ფუნქციას და ამცირებს მდგომარეობების სიმკვრივეს (მს). როდესაც ნანომესრის ზომები ახლოს არის დე ბროილის ტალღის სიგრძესთან, მს მცირდება მნიშვნელოვანად და იწვევს ფენის თვისებებში ცვლილებებს. მს-ის გათვლები არის რთული და დაკავშირებულია კვანტური ბილიარდის პრობლემასთან. ასეთი გათვლების შესრულება მოითხოვს დროზე დამოუკიდებელი შრედინგერის განტოლების ამონახსნების პოვნას დირიხლეს სასაზღვრო პირობებით. აქ ჩვენ ვიყენებთ რიცხვით მეთოდს, კერძოდ, დამხმარე გამომსხივებლების მეთოდს, რომელიც გთავაზობთ გამოთვლებთან დაკავშირებული რესურსების მნიშვნელოვან შემცირებას სხვა რიცხვით მეთოდებთან შედარებით
ამოცანა საკუთარ მნიშვნელობებზე
განვიხილოთ ელექტრომაგნიტური ტალღის დიფრაქცია ჩაკეტილ მეტალურ ზედაპირზე, რომელსაც გააჩნია ტალღის სიგრძესთან შედარებით ძალზე მცირე ხვრელი. ნახვრეტის სიმცირის გამო შიგა არეში ველი ფაქტიურად არ შედის, გამონაკლისს წარმოადგენს რეზონანსული სიხშირე, როდესაც დაცემული ველის სიხშირე და გამბნევი სხეულის საკუთარი ელექტრომაგნიტური რხევის სიხშირე ერთმანეთს ემთხვევა. ამ დროს ველი სხეულის შიგა არეში სწრაფად იწყებს ზრდას. შევნიშნოთ, რომ რეზონანსული სიხშირეები სხეულის გეომეტრიაზეა დამოკიდებული. ღია ნაწილის არ არსებობის შემთხვევაში ასეთ მოვლენას საერთოდ არა აქვს ადგილი. მიუხედავად ამისა აზრს არ არის მოკლებული ჩაკეტილი მეტალური ზედაპირების მიერ მოცულ არეებისთვის საკუთარი ველების და რხევის სიხშირეების პოვნა და გამოკვლევა, ვინაიდან ეს ორი შემთხვევა მჭიდროდ არის დაკავშირებული. განვიხილოთ ასეთი ტიპის ამოცანების მათემატიკური ასპექტები, კერძოდ მივმართოთ ისეთ მათემატიკურ ცნებას, როგორიც არის ოპერატორის საკუთარი მნიშვნელობა და მეთოდებს, რომლებიც მათ პოვნას ეხება. წრფივი ოპერატორის საკუთარი მნიშვნელობის განმარტება: წრფივ ვექტორულ L სივრცეზე (λ ველის მიმართ) განსაზღვრული A ოპერატორის საკუთარი მნიშვნელობა (ს.მ.) არის ველის ისეთი k ელემენტი, რომლისთვისაც არსებობს არანულოვანი ვექტორი x ∈ L, რომელიც Ax=kx პირობას აკმაყოფილებს. x ვექტორს ეწოდება A ოპერატორის λ საკუთარი
მნიშვნელობის საკუთარი ვექტორი. თუ ოპერატორი A წრფივია მაშინ მისი ს.მ. k ∈ λ ველის ისეთი ელემენტია, რომლისთვისაც ოპერატორი A-kI (სადაც I იგივური ოპერატორია) არაშებრუნებადია. თუ L ვექტორული სივრცე სასრულგანზომილებიანია მაშინ ს.მ.
სიმრავლე ემთხვევა det A kE=0 მახასიათებელი მრავალწევრის ფესვებს. აქ A არის წრფივი A გარდაქმნის მატრიცა რომელიღაც ბაზისში, ხოლო E ერთეულოვანი მატრიცაა. ს.მ. ჯერადობას უწოდებენ ამ მრავალწევრის ფესვების ალგებრულ ჯერადობას.
სასრულგანზომილებიანი სივრცის ნებისმიერი წრფივი გარდაქმნისას ს.მ. სიმრავლე არ არის ცარიელი თუ ეს სივრცე ალგებრულად ჩაკეტილია λ ველის მიმართ. ორივე პირობა, სასრულგანზომილობა და ალგებრულად ჩაკეტილობა არსებითია.
სასრულგანზომილებიანი სივრცის წრფივი გარდაქმნის ს.მ. ერთობლიობას წრფივი გარდაქმნის სპექტრი ეწოდება.
ხშირად, ფიზიკური მოვლენების აღსაწერად გამოიყენება დიფერენციალური ან ინტეგრალური ოპერატორები. განვიხილოთ ასეთი ტიპის ოპერატორების ს.მ. პოვნის ამოცანები. გამოვყოთ ეს ორი შემთხვევა.
დიფერენციალური ოპერატორებისთვის ს.მ. პოვნის მეთოდები სამ ძირითად ეტაპად იყოფა:
1) ამოცანის უფრო მარტივ, მაგალითად ალგებრულ (დისკრეტულ) სახემდე დაყვანა.
2) დისკრეტული ამოცანის სიზუსტის გამოკვლევა.
3) დისკრეტული ამოცანის ს.მ. გამოთვლა.
დისკრეტულ ამოცანამდე დაყვანა შესაძლებელია ძირითადად ბადის ან პროექციული მეთოდით. ამასთან ბუნებრივია მოვითხოვოთ რომ, დისკრეტულ ამოცანაში შენარჩუნებული იყოს ოპერატორის ძირითადი თვისებები. კერძოდ შესაბამისი ოპერატორის თვითშეუღლების თვისება, დისკრეტულ არგუმენტზე დამოკიდებულ ფუნქციათა სივრცეში.
ინტეგრალური ოპერატორების ს.მ.-ს პოვნის ამოცანა გულისხმობს ს.მ.-ს სრული სპექტრის ან ამ სპექტრის ნაწილის პოვნას. ხშირ შემთხვევებში საკმარისია ერთი ან ორი მოდულით მინიმალური ან მაქსიმალური მნიშვნელობების განსაზღვრა. ერთ-ერთ ყველაზე მნიშვნელოვან ამოცანას წარმოადგენს ფრედჰოლმის წრფივი ინტეგრალური ოპერატორის ს.მ. პოვნა. ეს ამოცანა მდგომარეობს ისეთი კომპლექსური λ რიცხვების პოვნაში, რომელთათვისაც არსებობს ინტეგრალური განტოლების არატრივიალური ამონახსნი (მოცემულ ფუნქციონალურ კლასში)
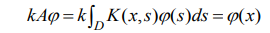
( ) L2 D , ან სხვა ფუნქციონალური სივრცეები, სადაც D არეა m R ევკლიდურ სივრცეში. ინტეგრალური განტოლების ს.მ. პოვნისთვის გამოიყენება ინტეგრალის აპროქსიმაცია. მაგალითად კვადრატურული ფორმულით აპროქსიმაციისას გვაქვს
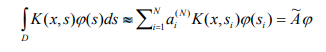
ამგვარად დგება საკითხი მატრიცის ს.მ. და შესაბამისი ფესვების პოვნისა:
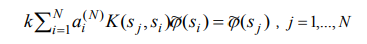
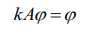
ამოცანა (3) ინტერპრეტირებულია, როგორც A ოპერატორთან მიახლოებული სხვა სივრცეში (რომელიც დაკავშირებულია
სივრცესთან) მოქმედი A ოპერატორის საკუთარ მნიშვნელობების პოვნის ამოცანა:
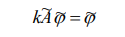
სიახლოვე. მაგალითის სახით მოვიყვანოთ შემდეგი: ვთქვათ გვაქვს სივრცეში მოქმედი An ოპერატორების მიმდევრობა და
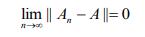
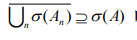
მუდმივებს, რომელთა მნიშვნელობები არ არის ცნობილი. სიზუსტის კონტროლის მიზნით შეიძლება გამოვიყენოთ ს.მ.–ების მიმდევრობა რომელიც იკრიბება საძიებელი ს.მ.-კენ. ასეთი მიმდევრობის აგება A ოპერატორთან A ოპერატორის თანდათან მიახლოებით მიზანშეწონილი არ არის, ვინაიდან ეს მოითხოვს გამოთვლების დიდი რაოდენობით ჩატარებას. მიღებული ს.მ.-თა სიზუსტე შეიძლება შეფასდეს ამოცანის მდგრადობის გამოკვლევით.
საკუთარი მნიშვნელობების პოვნა დამხმარე გამომსხივებლების მეთოდის გამოყენებით
განვიხილოთ ერთგვაროვანი სასაზღვრო ამოცანა G -ზე
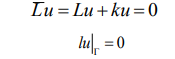
თუ არსებობს არატრივიალური ამონახსნი მოცემული ერთგვაროვანი ამოცანის, მაშინ u არის საკუთარი ფუნქცია, ხოლო
k L ოპერატორის საკუთარი მნიშვნელობაა. (ზოგჯერ ლიტერატურაში k -ს სასაზღვრო (6)(7) ამოცანის საკუთარ მნიშვნელობას უწოდებენ).
ოპერატორის ფუნდამენტური ამონახსნები აღვნიშნოთ K(z, x, k) , სადაც E ერთეულოვანი ოპერატორია [3] . ვთქვათ

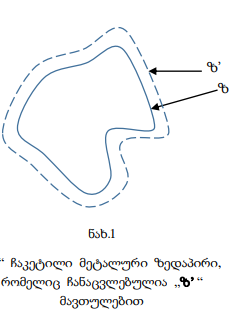
ყველგან მკვრივად მდებარეობს ზ’ ზედაპირზე (იხ. ნახ.1) სასაზღვრო ამოცანის მიახლოებითი ამონახსნი ვეძებოთ შემდეგი სახით
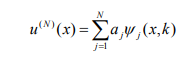
სადაც (x,k) j ერთი ინდექსის საშუალებით გადანომრილი ფუნქციებია (8)-დან. (9)-ი(7)-ში ჩასმით და რაიმე ფუნქციონალების ტოტალური სისტემის პირველი N წრფივი 9 ფუნქციონალების გამოყენებით მივიღებთ j a კოეფიციენტების გამოსათვლელ N რიგის წრფივ განტოლებათა სისტემას:
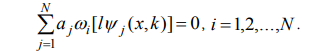
იმისათვის, რომ ამ სისტემას ჰქონდეს არატრივიალური ამონახსნი, აუცილებელია მისი დეტერმინანტი ნულის ტოლი იყოს:
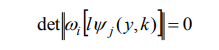
ამ ტრანსცენდენტული განტოლების ფესვები მიახლოებით განსაზღვრავენ L ოპერატორის საკუთარ მნიშვნელობებს.
L ოპერატორის საკუთარი მნიშვნელობების პოვნის განხილული მიდგომა ემყარება იმ მოსაზრებას, რომ
l (y, k) j ფუნქციები, სადაც (y, k) j L ოპერატორის ფუნდამენტური ამონახსნებია, ქმნიან წრფივად დამოუკიდებელ სისტემას იმ შემთხვევაში, როცა k განსხვავებულია L ოპერატორის საკუთარი მნიშვნელობებისგან. კერძოდ, როცა
i ფუნქციონალები განმარტებულია სკალარული ნამრავლით L2(ზ) ჰილბერტის სივრცეში, მაშინ (5)-ის მარცხენა ნაწილი იქნება წრფივად დამოუკიდებელი l (y, k) j სისტემის გრამის დეტერმინანტი, რომელიც არ შეიძლება იყოს ნულის ტოლი. ამგვარად (9) განტოლების ყველა ფესვი იქნება L ოპერატორის საკუთარი მნიშვნელობები.
ოპერატორის საკუთარი მნიშვნელობების პოვნის მეთოდის რიცხვითი რეალიზაცია მნიშვნელოვან გამოთვლით სირთულეებს აწყდება, გრამის დეტერმინანტის სიმცირის და (10) განტოლების ტრანსცენდენტულობის გამო, რომლის ფესვებიც საკუთარი მნიშვნელობებია.
განვიხილოთ განსხვავებული მიდგომა საკუთარი მნიშვნელობების საპოვნელად, რომელიც შესაბამისი მატრიცის დეტერმინანტის ნულების პოვნის მაგიერ გულისხმობს ელექტრომაგნიტური ტალღის დიფრაქციის ამოცანის ამოხსნით რეზონანსული სიხშირეების პოვნას exp( it) (დროითი დამოკიდებულება). მონოქრომატული ელექტრომაგნიტური ტალღის დიფრაქციის ამოცანა იდეალურად
გამტარ ან დიელექტრიკულ სხეულებზე და ამ სხეულების ზედაპირებით შემოსაზღვრულ არეებში რეზონანსული სიხშირის განსაზღვრის ამოცანა, ერთმანეთთან მჭიდრო კავშირშია. მათემატიკური თვალსაზრისით პირველი ამოცანა დაიყვანება ჰელმჰოლცის განტოლების
(11) ამოხსნაზე არაერთგვაროვანი სასაზღვრო პირობებით (12)

სადაც f (r) საზღვარზე მოცემული ფუნქციაა. ხოლო მეორე _ ერთგვაროვანი სასაზღვრო პირობებით
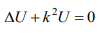
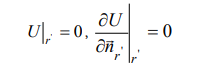
ლაბორატორიაში. გამოყენებული იყო დ.გ.მ.-ით ტალღგამტარების თვისებების შესასწავლად [4]. მაგალითისთვის განვიხილოთ ამოცანა, რომელიც დაგვეხმარება მეთოდის არსის გადმოცემაში. ვთქვათ გვაქვს N რაოდენობის, მცირე ელექტრული რადიუსის kao 1 , იდეალური გამტარები, რომლებიც თანაბრად არიან განლაგებულნი რაიმე „ზ’ “ ზედაპირზე, n 1,2,…N. (ნახ.1).
ვთქვათ, სისტემას ეცემა მონოქრომატული ელექტრომაგნიტური ტალღა, რომელშიც ელექტრული ველის დაძაბულობის ვექტორია
E (x, y,z) i. მთელ სივრცეში (გარდა n r წერტილებისა) სრული ველის ელექტრული დაძაბულობის ვექტორი შეიძლება
წარმოდგენილი იყოს შემდეგი სახით:
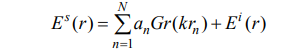
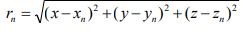
მანძილი n -ური მავთულიდან დაკვირვების წერტილამდე. უცნობი an დენის სიმკვრივეები განისაზღვრება სასაზღვრო პირობებიდან.
გაბნეული ველის ტალღურ რიცხვზე დამოკიდებულების შესწავლა უჩვენებს, რომ [3,4,5] : ტალღურ რიცხვთა რაღაც
{ }i k თვლადი რაოდენობის მნიშვნელობების და მათი მიდამოების გარდა (14) ფორმულით გამოთვლილი გაბნეული ველი, გამტარების N
ნახ.1 „ზ“ ჩაკეტილი მეტალური ზედაპირი, რომელიც ჩანაცვლებულია „ზ’ “ მავთულებით ზ’ ზ 11 რიცხვის გაზრდით, სწრაფად მიისწრაფის „ზ“ უწყვეტი ზედაპირის მიერ გაბნეული ველისკენ.
- ტალღური რიცხვის { }i k k ზოგიერთ მნიშვნელობაზე ველი რეზონატორის შიგნით მკვეთრად იზრდება და გამტარი მავთულების რიცხვის ზრდით ის მიისწრაფის „ზ ზედაპირის მქონე ღრუ რეზონატორის საკუთარი ველისკენ. ამ შემთხვევაში i k მიისწრაფის, ამ ზედაპირით შემოსაზღვრული D არისთვის დირიხლეს ამოცანის საკუთარი მნიშვნელობისკენ, ანუ ამ რეზონატორის რეზონანსული სიხშირეებისკენ.
- ტალღური რიცხვის { }i k მნიშვნელობების მახლობლობაში მავთულოვანი რეზონატორის მიერ გაბნეული ველი შეიძლება წარმოდგენილ იქნეს ორი ველის სუპერპოზიციის სახით
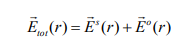
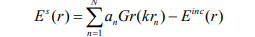
აღწერს ველს სხეულის გარეთ, რომელიც გამტარების რაოდენობის ზრდით მიისწრაფის უწყვეტი ზედაპირიდან გაბნეული ველისკენ, ხოლო შიგა არეში ნულისკენ. მანქანური გამოთვლების დროის შემცირების მიზნით მოცემული ამოცანის ამოსახსნელად შესაძლებელია დამხმარე გამომსხივებლების მეთოდის გამოყენება, თუ გამოყოფილი არეებისთვის შესაბამისად აგებული იქნება დამხმარე ზედაპირები. საკუთარი მნიშვნელობების პოვნის აღწერილ მიდგომას ვიყენებთ ჩაკეტილი ზედაპირით შემოსაზღვრულ ღრუ გამტარი სხეულების ელექტროდინამიკური თვისებების შესასწავლად.
აღვნიშნოთ რომ, დ.გ.მ.-ის ძირითადი არსი მდგომარეობს უცნობი ველის წარმოდგენაში შესაბამისი ტალღური განტოლების ფუნდამენტური ამონახსნების ჯამის სახით, რომელთა წყაროები განლაგებულია იმ არის გარეთ მდებარე დამხმარე ზედაპირზე, სადაც უნდა განისაზღვროს ველი. გაბნეული ველის ასეთი წარმოდგენა შესაძლებელია სანამ არსებობს გაბნეული ველის ანალიზური გაგრძელება. საძიებელი ველის ფუნქცია წყაროსა და დამხმარე გამომსხივებლების ფუნქციების ჯამის სახით შემდეგნაირად წარმოიდგინება:
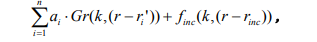
პერიოდული გრინის ფუნქცია
ველისთვის, რომელიც ერთი ნებისმიერი მიმართულებით ერთგვაროვანია, ამოცანა დაიყვანება ორგანზომილებიან შემთხვევაზე. x ღერძზე განლაგებული პერიოდული მონოპოლური წყაროების მიერ შექმნილი ელექტრული ვექტორ პოტენციალის ველი 𝐴⃗⃗
მოიცემა შემდეგი ჯამით:
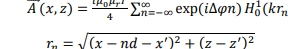
𝜇𝑟 არის ფარდობითი მაგნიტური ამთვისებლობა მოცემული გარემოსთვის. 𝜇0 მაგნიტური კონსტანტაა. 𝐻0 1 არის პირველი რიგი ჰანკელის ფუნქციაში. x მიმართულებით d არის მონოპოლების მასივის პერიოდი. Δ𝜑 არის ფაზური წანაცვლება. (15) ჯამი ცუდად
კრებადია.
პუასონის კრებადობის ფორმულა
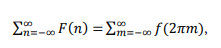

პერიოდული გრინის ფუნქცია გამტარი გარემოს შემთხვევაში
ამ თავში აღწერილია დამხმარე გამომსხივებლების მეთოდში გამტარი გარემოს შემთხვევაში პერიოდული გრინის ფუნქციის გამოყენების რიცხვითი თავისებურებანი. კერძოდ გამტარი გარემოს აღსაწერად, მოდელში 𝑘 ტალღური რიცხვი ხდება კომპლექსური. ამ შემთხვევაში (16) ფუნქციის კრებადობა „კატასტროფულად“ ფუჭდება, ხოლო (15)-ისა მნიშვნელოვნად უმჯობესდება. ამგვარად გამტარი გარემოს მოდელში მიზანშეწონილია (15)-ის გამოყენება. გარდა ამ გარემოებისა, რიცხვითი რეალიზაციის დროს სტაბილური ამონახსნების მისაღებად მნიშვნელოვანი გახდა (15)-ის კრებადობის შეფასება მოხდეს, როცა |𝑛| > с, სადაც с მინიმალური მნიშვნელობის დადგენა ხდება რიცხვითი ექსპერიმენტებით. სხვა მხრივ დამხმარე გამომსხივებლების მეთოდის გამოყენების სქემა უცვლელი რჩება ამ ამოცანის ამოსახსნელად.
გეომეტრიის აღწერა
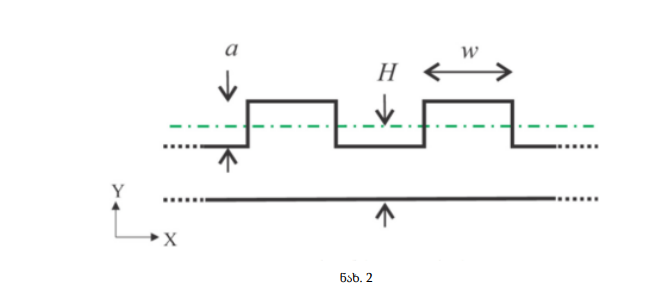
ნაშრომში განხილულია პერიოდული მართკუთხა იმპულსების მსგავსი ფორმის კონტურებით შემოსაზღვრული არეები. ნახ.2 გვიჩვენებს ნანომესრული არის ტიპურ ჭრილს. ზედაპირულ მესერს აქვს სიღრმე a და სიგანე w. შედარებისთვის აღებულია H სისქის ბრტყელი ფენა, რომელსაც იგივე ჭრილი გააჩნია. ნანომესრული ფენა არის კვაზი1D სისტემა 0
გამოთვლების შედეგები
ამ თავში მოცემულია პრაქტიკული გამოთვლების გრაფიკული შედეგები. x ღერძზე მოიცემა ტალღური რიცხვები 3-10 შუალედში, რომლებიც დათვლილია 2000 დისკრეტული წერტილისთვის. გრაფიკებზე ასახულია რეზონანსები და მისი შესაბამისი ტალღური რიცხვები. განხილულია სხვადასხვა გეომეტრია, რომლებიც ერთმანეთისგან პერიოდითა და მესრის a სიღრმით განსხვავდება.
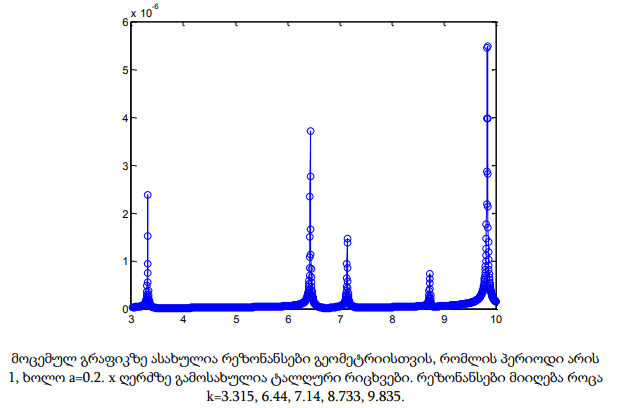

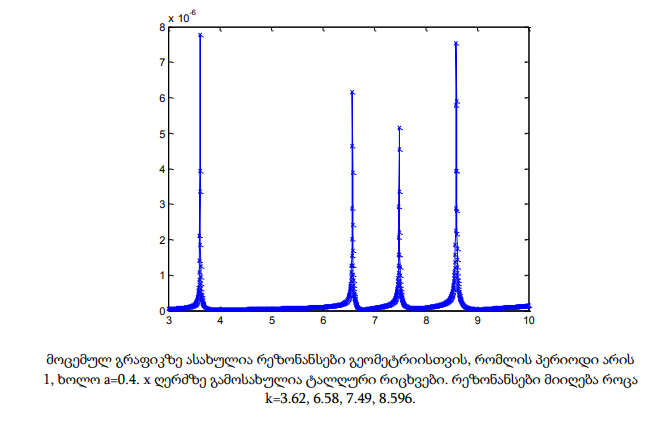
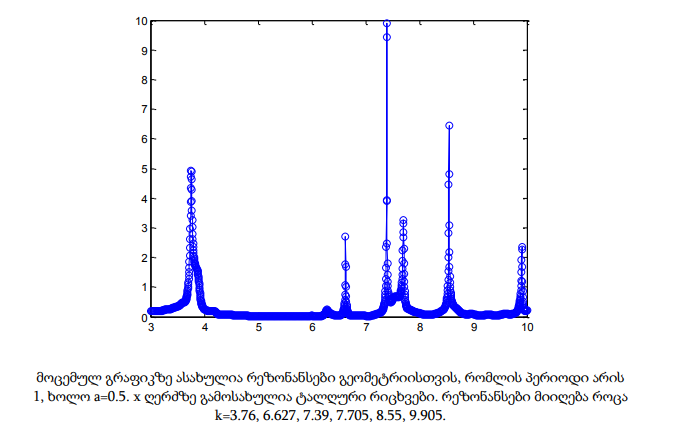
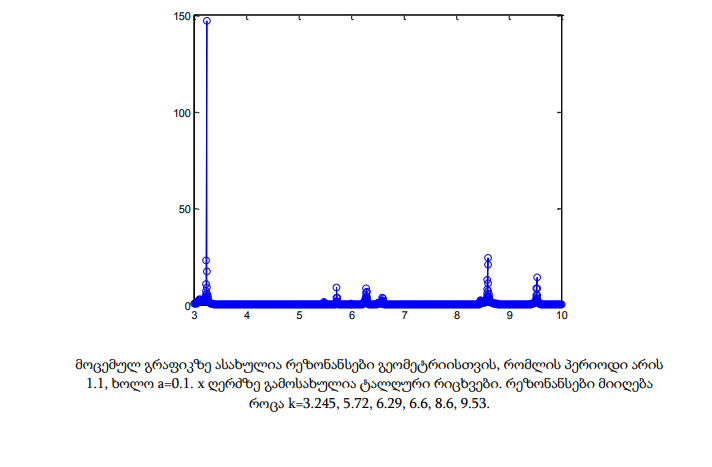
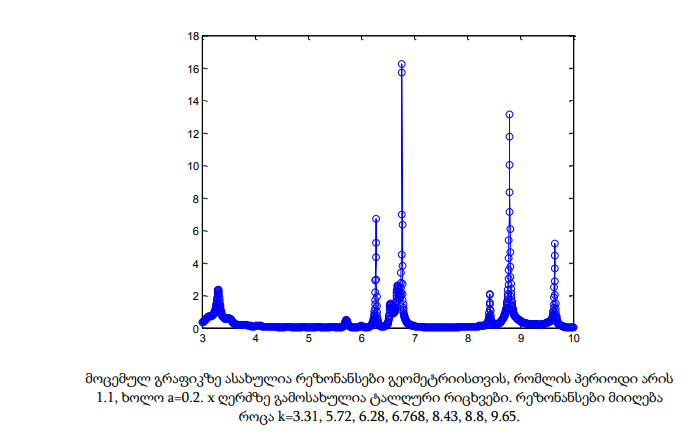
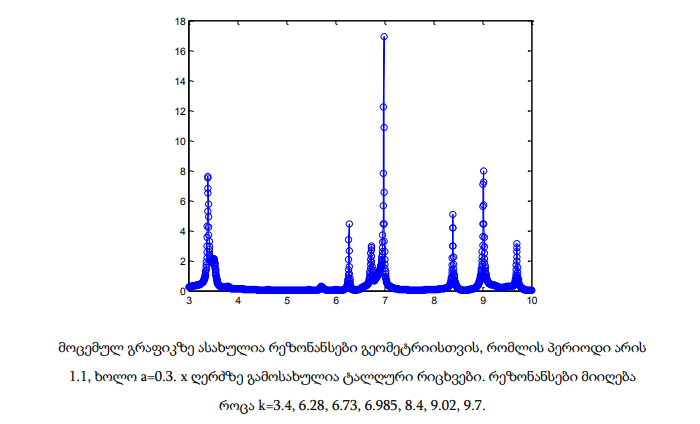
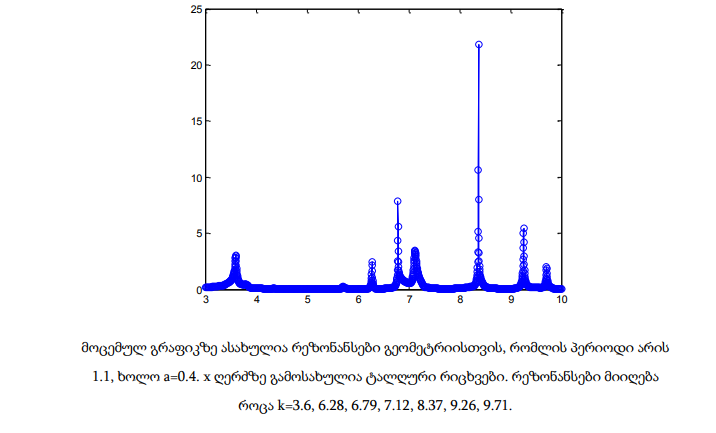
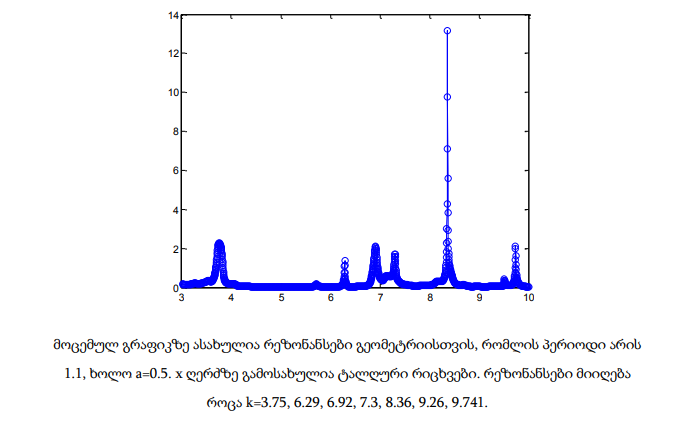

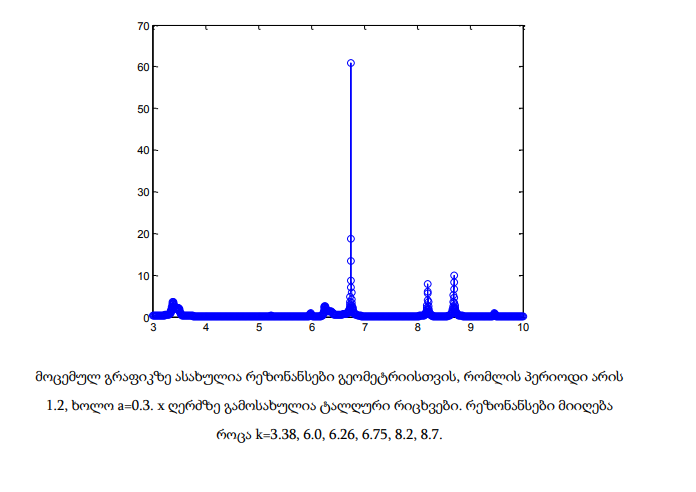
მოცემულ თავში განხილული რეზონანსული სიხშირეების პოვნის მეთოდი ძალზედ ეფექტურია რიცხვითი რეალიზაციის თვალსაზრისით. მისი ძირითადი არსი ფიზიკური მოსაზრებებიდან გამომდინარეობს. მეთოდის საშუალებით ადვილად განისაზღვრება
პირველი რეზონანსები. საკუთარი მნიშვნელობების პოვნასთან ერთდროულად ხდება საკუთარი ფუნქციების მიღებაც. საკუთარი მნიშვნელობების გამოსაკვლევად მეთოდისთვის საჭირო უცნობების რაოდენობა სუსტად არის დამოკიდებული სიხშირეზე.
საკუთარი მნიშვნელობების დაზუსტება დამხმარე ზედაპირის დაშორებითაც არის შესაძლებელი. ასევე მეთოდით შესაძლებელია რეზონანსული დენის განაწილების პოვნა. ტესტური ამოცანების ამოხსნით მიღებული შედეგები კარგ თანხვედრაშია თეორიულ მონაცემებთან, რაც ადასტურებს მეთოდის უპირატესობას ასეთი ტიპის ამოცანების ამოსახსნელად ტრადიციულ მეთოდებთან შედარებით. ასევე მოცემული მიდგომით გამოკვლეულია რთული გეომეტრიული ფორმის ჩაკეტილი მეტალური ზედაპირის მიერ
მოცული არისთვის საკუთარი მნიშვნელობები, საკუთარი ველები და დენის განაწილებები. მეთოდის პრაქტიკული გამოყენება ფართო შესაძლებლობებს იძლევა რეზონანსული სტრუქტურების თვისებების გამოსაკვლევად.
ავტორი: ნოდარ საზანდრიშვილი
გამოყენებული ლიტერატურა:
- D. Kakulia, A. Tavkhelidze, V. Gogoberidze, M. Mebonia, Density of quantum states in
quasi-1D layers. - D. Kakulia, K. Tavzarashvili, G. Ghvedashvili, D. Karkashadze and Ch. Hafner, The Method
of Auxiliary Sources Approach to Modeling of Electromagnetic Field Scattering on TwoDimensional Periodic Structures. - Алексидзе М.А. “Фундаментальные функции уравнений математической физики в
приближонних решениях граничных задач” часть I. Изд. ТУ Тбилиси 1989. с 158-179. - Zaridze R. Karkashadze D. Khatiashvili J. Method of Auxiliary Sources for investigation of
along-regular waveguids 1985 Tbilisi State University 150 p. - R. Zaridze, D. Kakulia, K. Tavzarashvili, A. Bijamov, G. Ghvedashvili, G. Chelidze,
“Determination of Eigenvalues of The Object Using The Method Of Auxiliary Sources
(MAS)”. Proceedings of VIth International Seminar/Workshop on Direct and Inverse
Problems of Electromagnetic and Acoustic Wave Theory (DIPED-2001), Lviv, Ukraine,
September 18-20, 2001, pp. 183-190.
