სიმძიმის ძალის განაწილების ხასიათი დედამიწის ზედაპირზე ქერქის აგებულებაზეა დამოკიდებული. ამიტომ, თუ ვიცით ეს განაწილება, შეიძლება ვიმსჯელოთ ქერქის აგებულებაზეც. პირველი გეოფიზიკური თეორია ქერქის აგებულების შესახებ, რომელიც XIX საუკუნის შუა წლებში ჩამოყალიბდა, წარმოიშვა გრადუსული გაზომვების შედეგების დამუშავების დროს გამოვლენილი შეუსაბამობის ახსნასთან დაკავშირებით; მას იზოსტაზიის ანუ დედამიწის ქერქის წონასწორობის თეორია ეწოდა.
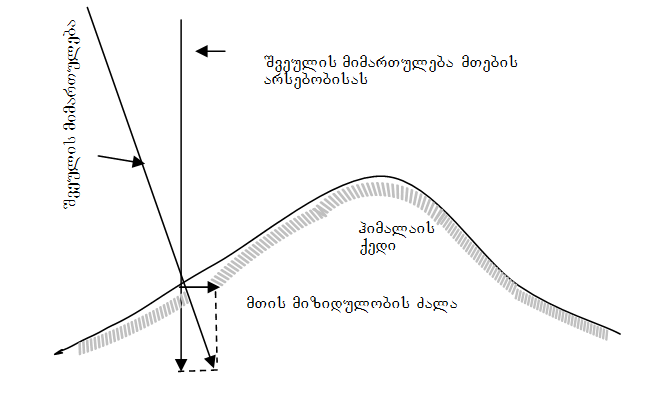

ცხრილში ყველაზე საყურადღებო ფაქტი ის არის, რომ გაზომილი მნიშვნელობები გაცილებით ნაკლებია თეორიულად გამოთვლილ მნიშვნელობებზე. რით უნდა აიხსნას ეს განსხვავება? ჰიმალაის ქედი და მის მიერ შექმნილი მიზიდულობის ძალის ჰორიზონტული მდგენლი რეალობაა, რაშიც ეჭვს ვერ შევიტანთ. იმისათვის კი, რომ შევამციროთ მიზიდულობის ძალის ჰორიზონტული მდგენელი და გავათანაბროთ გამოთვლილი და გაზომილი მნიშვნელობები, საჭიროა დაუშვათ, რომ ჰიმალაის ქედის ქვეშ არსებობს უარყოფითი მასა, რომელიც მიზიდულობის ძალას აკომპენსირებს. გაეცნო რა პრატის ამ რეზულტატებს, გრინვიჩის ასტრონომიული ობსერვატორიის დირექტორმა ე რ ი მ (1855) წარმოადგინა მოდელი, რომლის საშუალებითაც შეეცადა ამ ამოცანის გადაწყვეტას.
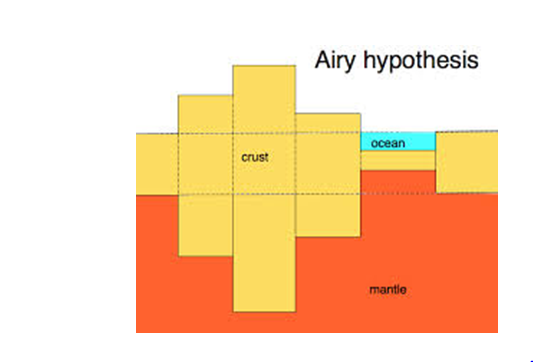
ამ მოდელის თანახმად დედამიწის ქერქი, შედგენილი შედარებით მსუბუქი ნივთიერებისაგან რომელსაც ს ი ა ლ ი (SiAl) ეწოდება, ცურავს უფრო მკვრივ და ბლანტ ნივთიერებაზე, რომელსაც ს ი მ ა (SiMa) ეწოდება. ქერქი დაყოფილია სვეტებად, რომლებსაც ერთნაირი სიმკვრივე და სხვადასხვა მასა აქვს.
სვეტები ტივტივებს ასევე ერთგვაროვან, მაგრამ უფრო მკვრივ და ბლანტ სიმაზე. ერის მიხედვით მთათა ქედები – ეს არის დედამიწის ქერქის შესქელება, რომელიც არა მარტო ზევითარის ამოწეული, არამედ ქვევით სიმაშიაც იძირება, ამიტომ, ამ ქედების ქვეშ, უფრო მკვრივი სიმას ნაცვლად ადგილს იკავებს ნაკლებად მკვრივი სიალის სვეტი. სიალის სვეტის მასა კი სიმასთან შედარებით უარყოფითია და ამით ქედის მიზიდულობის ეფექტური ძალა მცირდება. თუ სიალის სიმკვრივეს აღვნიშნვთ s0-ით, სიმას s-თი, დედამიწის ქერქში ამოკვეთილი სვეტის სისქეს B-თი ხოლო მასში ჩაძირვის სიღრმეს b-თი, მაშინ არქიმედის კანონის თანახმად
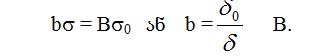
აქედან სიმას ზევით მოთავსებული სვეტის სიმაღლე იქნება:
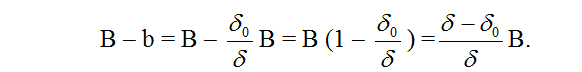
ერის ნაშრომის გამოქვეყნებიდან რამოდენიმე წლის შემდეგ პრატმა სხვა მოდელი შექმნა (1859), სადაც მან ერისაგან განსხვავებით დაუშვა, რომ დედამიწის ქერქის სიმკვრივე ერთნაირი არ არის; კერძოდ ის უფრო მცირეა იქ სადაც ქერქი ნაკლებად შეიკუმშა, მაგალითად მთების ქვეშ და პირიქით, ქერქი უფრო მკვრივია ძლიერი შეკუმშვის ადგილებში, მაგალითად ზღვების ქვეშ. ამავე დროს არსებობს გარკვეული სიღრმე, რომლის ზევით მოქცეული ნივთიერების წონა (იქნება ეს მაღალი მთები თუ ღრმა ზღვები) ერთნაირი ხდება. პრატი თვლიდა, რომ ეს სიღრმე დაახლოებით 200 კმ-ის ტოლია. პრატის მოდელშიც, ისევე როგორც ერის მოდელში ქედების ქვეშ სიალის მასა სიმასთან შედარებით უარყოფითია, რაც ასევე ხსნის შვეულის გადახრის მოვლენას. პრატმაც ერის მსგავსად დედამიწის ქერქი ერთნაირი განივკვეთის მქონე ვერტიკალურ სვეტებად დაჰყო, რომლებიც სხვადასხვა სიმკვრივისა და მოცულობის, მაგრამ ტოლ მასებს შეიცავს.
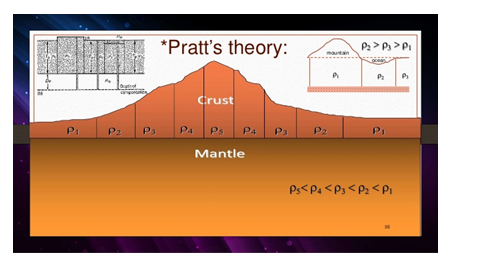
ერის ჰიპოთეზაში ჰიდროსტატიკურ გათანაბრებას ადგილი აქვს CD ზედაპირზე, რომელიც ყველაზე ღრმა სვეტის ქვეშ გადის და ამ ზედაპირს სვეტები თანაბარი ძალით აწვება.
დაუშვთ ეს ზედაპირი CD ზღვის დონის ქვემოთ T სიღრმეზე ძევს, რელიეფის სიმაღლეა H; როცა H=0, მაშინ ვერტიკალური სვეტის სიმკვრივეა s0, ხოლო როცა H ¹0, მაშინ ვერტიკალური სვეტის სიმკვრივეა s. მაშინ, რადგან ყველა სვეტის მასა ტოლია, გვექნება:
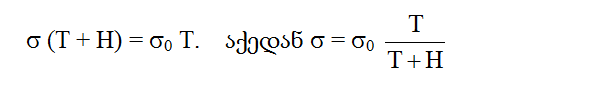
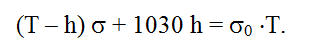
სადაც h ზღვის სიღრმეა, ხოლო 1030 კგ/მ3 ზღვის წყლის სიმკვრივე, აქედან
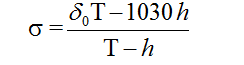
ამ ფორმულების საფუძველზე ჩატარებული გაანგარიშება გვიჩვენებს, რომ მთის ქვეშ, რომლის საშუალო სიმაღლე 6 კმ-ია, სვეტის საშუალო სიმკვრივეა 2520 კგ/მ3, ხოლო ოკეანის ქვეშ, რომლის სიღრმე საშუალოდ 5 კმ-ია – 2760 კგ/მ3.
განხილულ ჰიპოთეზებს შორის ის ძირითადი განსხვავებაა, რომ პრატის სქემაში მაკომპენსირებელი მასები თანაბრადაა განაწილებული ვერტიკალური სვეტების მთელ სიმაღლეზე. ხოლო ერის სქემაში ეს მასები განაწილებულია სვეტების ფუძეებისაგან შედგენილ ზედაპირსა და ჰიდროსტატიკური გათანაბრების ზედაპირს შორის. სხვაგვარად, იზოსტაზიური კომპენსაცია წარმოებს ქერქის სიმკვრივის ცვალებადობის (პრატის ჰიპოთეზა) ან მისი სიმძლავრის ცვალებადობის გამო (ერის ჰიპოთეზა). სინამდვილეში ეს ორივე ფაქტორი ერთდროულად არსებობს რეალურ ქერქში და მონაწილეობს მის წონასწორობაში.
უნდა აღინიშნოს, რომ ორივე ჰიპოთეზა ზედმიწევნით სქემატურია და მთელი რიგი მნიშვნელოვანი დეფექტებით ხასიათდება. ასე მაგალითად, დაშვებულია, რომ სვეტებს, როგორი მცირე განიკვეთისაც არ უნდა იყოს, აქვს ვერტიკალური გადაადგილების უნარი, ვიდრე წონასწორობა არ დამყარდება. აქ უგულვებელყოფილია სვეტებს შორის ხახუნის ძალა და ის გარემოება, რომ სვეტები დედამიწაში თაღს ქმნის, რაც თავის მხრივ მათი მოძრაობის საწინააღმდეგო პირობებს ქმნის.
ამ დეფექტების ნაწილობრივ მაინც თავიდან ასაცილებლად შემოღებულ იქნა ცნებები ლოკალური და რეგიონული მასშტაბის განივკვეთის მქონე სვეტების გაწონასწორების შესახებ. პირველი მათგანი გულისხმობს მცირე განივკვეთის მქონე სვეტის, ხოლო მეორე – მხოლოდ დიდი (1000 კმ2 და მეტი) განივკვეთის მქონე სვეტის დამოუკიდებლად გაწონასწორებას. ეს უკანასკნელი შეიძლება შეიცავდეს მცირე ზომის გაუწონასწორებელ სვეტებსაც.
გარდა ზემოთქმულისა, აღწერილ იზოსტაზიურ სქემებში არ არის გათვალისწინებული გარემოება, რომ სიღრმის მიხედვით ფენის სიმკვრივე იზრდება. ამიტომ იყო ცდა იზოსტაზიის პრინციპზე დაყრდნობით წარმოედგინათ დედამიწის ქერქში სიმკვრივის განაწილების უფრო მართებული სურათი. მაგალითად, ფინელი გეოდეზისტის ჰეისკანენის წარმოდგენით სიალის, ისევე როგორც სიმას შემადგენელი ქანების სიმკვრივე სიღრმის მიხედვით ნახტომისებურად იზრდება.
ერისა და პრატის ჰიპოთეზების განხილვისას ბუნებრივად ისმება კითხვა, რომელი ჰიპოთეზა უფრო ადვილად ხსნის გრავიტაციული ანომალიების არსებობას? მათემატიკური თვალსაზრისით, ორივე ჰიპოთეზა ერთნაირ, დამაკმაყოფილებელ შედეგს იძლევა. სამაგიეროდ, გეოლოგიური თვალსაზრისით ერის ჰიპოთეზა უფრო ახლოა სინამდვილესთან, რაც თანამედროვე კვლევებითაც დასტურდება
1931 წელს ჰოლანდიელმა გეოფიზიკოსმა ვენინგ-მეინესმა შეიმუშავა იზოსტაზიის მოდერნიზებული ჰიპოთეზა. მან დედამიწის ქერქი წარმოიდგინა, როგორც მაგმაში მცურავი დრეკადი ფირფიტა, რომელიც მთების ქვეშ ჩაზნექილია და ეს ჩაზნექვა მანამ გრძელდება, ვიდრე წონასწორობის მდგომარეობა არ დამყარდება (ნახ. 3.21). ჩაზნექვის სიდიდე, რომელიც პროპორციულია: 1. დამატებითი მასისა; 2. ქანების დრეკადი თვისებისა და 3. დედამიწის ქერქის სიმძლავრისა, შეიძლება გამოანგარიშებულ იქნას დრეკადობის თეორიის გამოყენებით. ამგვარად , სიალის ჩაზნექილი ნაწილი იკავებს გამოდევნილი სიმას ადგილს. ვენინგ-მეინესის მიხედვით იზოსტაზიური წონასწორობა ორგვარად შეიძლება დამყარდეს: ა. სიალის სიმკვრივე მუდმივია, მაშინ კომპენსაცია ერის ჰიპოთეზის მიხედვით ხდება და ბ. სიალის სიმკვრივე სიღრმის მიხედვით თანდათან იზრდება, ვიდრე სიმას სიმკვრივეს არ გაუტოლდება.
მართალია, იზოსტაზიური თეორიები სქემატურია, მაგრამ მიუხედავად ამისა სიმძიმის ძალის ანომალიების შესწავლისას ვრწმუნდებით, რომ დედამიწის ქერქი მთლიანად, ან დიდ რეგიონებში, მართლაც მიისწრაფის წონასწორობისაკენ ერის თეორიის შესაბამისად. იზოსტაზიური წონასწორობის დარღვევა გეოტექტონიკური პროცესის ერთ-ერთი შედეგია და მოწმობს, რომ ეს პროცესი დღესაც მიმდინარეობს. ამის ნათელ დადასტურებას წარმოადგენს ეგრეთწოდებული ბუნებრივი იზოსტაზიური ექსპერიმენტები. ცნობილია, რომ დედამიწის ზოგიერთ რაიონში რელიეფი სწრაფად იცვლება. მაგალითად დღეისათვის ფინეთსა და სკანდინავიაში, აგრეთვე კანადის ჩრდილო ნაწილში ხმელეთის ზედაპირი იწევს მაღლა მაქსიმალური სიჩქარით 1 სმ/წელიწადში.
განვიხილოთ ხმელეთის ამოზევების საინტერესო მაგალითი ფენოსკანდიაში (ფინეთი + სკანდინავია). მართლაც, თუ გავზომავთ ძველი სანაპირო ზოლის სიმაღლის ნიშნულებს ფენოსკანდიის სხვადასხვა რაიონში შეიძლება განისაზღვროს ხმელეთის ამოზევების როგორც სიდიდე ისე სიჩქარე. გეოლოგების საერთო აზრით, რომლების მეოთხეულ ნალექებს სწავლობენ, პლეისტოცენური გამყინვარების შემდეგ ხმელეთის ზედაპირი ამ რეგიონში 500 მ-ით აიწია. რასაკვირველია ამოზევების სიჩქარის დადგენის ყველაზე ზუსტ მეთოდს გეოდეზიური წარმოადგენს. მართლაც, ნიველირების შედეგებმა, რომელიც 30-40 წლის ინტერვალით ტარდებოდა აჩვენა, რომ ბოტნიის სრუტის შუა ნაწილში ეს სიჩქარე ტოლია 9 მმ-სა წელიწადში. ეს მნიშვნელობა პერიფერიებისაკენ ნელ-ნელა მცირდება. ნულოვანი კონტურის შემდეგ ხმელეთი დაძირვას იწყებს, თუმცა საკმაოდ ნელა. რატომ ხდება ხმელეთის აზევება და დაძირვა? ეს მოვლენა შემდეგნაირად შეიძლება ავხსნათ. უკანასკნელი გამყინვარების დროს ფენოსკანდია დატვირთული ყინულის მძლავრი საფარით (რომლის სიმძლავრე ( 2,5 კმ იყო) ჩაიძირა მანტიაში დაახლოებით 600-700 მეტრით. ყინულის დადნობის შემდეგ (დაახლოებით 10 000 წლის წინად), ჰიდროსტატიკური წონასწორობის პრინციპის შესაბამისად რეგიონმა ამოზევება დაიწყო. ცენტრალურ რაიონში ამოზევება და პერიფერიულში დაძირვა დღესაც გრძელდება. სხვა სიტყვებით რომ ვთქვათ, საქმე გვაქვს იზოსტაზიის ცოცხალ მაგალითთან. ამ პროცესის ძირითადი შედეგი ის არის, რომ დღეს ქერქქვეშა მასალის დინება მიმართულია ცენტრალური ზეგანისაკენ. მყინვარმა გამოიწვია ლითოსფეროს ჩაღუნვა და ასტენოსფეროს ნივთიერების გვერდებზე გადადენა. მანტიის საკმაოდ დიდი სიბლანტის გამო, მყინვარის გადნობის შემდეგ ლითოსფეროს ჩაღუნვა ჯერ კიდევ არ არის კომპენსირებული და ამ ტერიტორიაზე დაიკვირვება სიმძიმის ძალის უარყოფითი ანომალია. ბოტნიურ სრუტეზე საშუალო ამპლიტუდა დაახლოებით –10-დან –15-მდე მგალის რიგისაა. თუ ჩავთვლით, რომ უარყოფითი ანომალია განპირობებულია მანტიის მასალის დეფიციტით (s=3300 კგ/მ3), რომელიც ჯერ კიდევ უნდა მოედინებოდეს ზეგანის ცენტრალური ნაწილისაკენ. ნარჩენი იზოსტაზიური აზევების h სიმაღლე შეიძლება გამოვიანგარიშოთ უსასრულო გავრცელების ჰორიზონტული ფენის მოზიდულობის ძალის ფორმულიდან
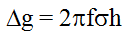
იზოსტაზიური ექსპერიმენტების სხვა მაგალითებს ვხვდებით გრენლანდიასა და ანტარქტიდაში. ხმელეთის ზედაპირი, სანამ ის გადაიფარებოდა ყინულის მძლავრი ფენით, ალბათ ზღვის დონის ზევით მდებარეობდა, უფრო გვიან, ყინულის დაწნევის გამო, ხმელეთის ზედაპირი ზღვის დონის ქვევით ჩაიძირა იზოსტაზიური წონასწორობის შენარჩუნებისათვის. ამგვარად, გრენლანდიასა და ანტარქტიდაში ჩვენ ვხვდებით ბუნებრივი ექსპერიმენტის პირველ, ხოლო ფენოსკანდიაში – მეორე ფაზას.
ამონარიდი დედამიწის ფიზიკიდან
