შრედინგერის განტოლება, რომელიც ითვალისწინებს ყველა სახის ურთიერთქმედებას მრავალელექტრონიან ატომში, არ იხსნება ანალიზურად და არც რიცხობრივად. თუმცა, ეს ურთიერთქმედებები შეიძლება განვალაგოთ გარკვეული იერარქიული მიმდევრობით და შემდგომ გავითვალისწინოთ ისინი თანმიმდევრობით შეშფოთების თეორიის ფარგლებში. თუ გავითვალისწინებთ მხოლოდ ელექტრონების ბირთვთან და ერთმანეთთან ელექტროსტატიკურ ურთიერთქმედებას შრედინგერის განტოლება შეიძლება ჩავწეროთ შემდეგი სახით
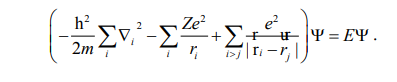
აქ პირველი წევრი ელექტრონების კინეტიკური ენერგის ოპერატორების ჯამია, ხოლო მეორე და მესამე წევრები ელექტრონების ბირთვთან და ერთმანეთთან ურთიერთქმედების პოტენციალური ენერგიის ოპერატორებია.
ელექტრონების ელექტროსტატიკური ურთიერთქმედება ბირთვთან წარმოადგენს ყველაზე მნიშვნელოვან ურთირთქმედებას, რომელიც განსაზღვრავს ატომის გარსულ მოდელს. ამ ურთიერთქმედების ენერგია დაახლოებით Z2–ის პროპორციულია. ელექტრონების ელექტროსტატიკური ურთერთგანზიდვა დაახლოებით Z-ის პოპორციულია. ეს ურთიერთქმედება განხილვის პირველ ეტაზე
შეიძლება ან უგულებელყოფილი იყოს, ან ჩანაცვლეს ეფექტური ცენტრალური სიმეტრიის მქონე პოტენციალით. ამ გზით პოულობენ ერთელექტრონიან მდგომარეობებს – ენერგიებს და ტალღურ ფუნქციებს. ასეთი მიდგომით მრავალელექტრონიანი ამოცანა დაიშლება რამდენიმე ერთელექტრონიან ამოცანად, თითოეულ ამოცანა თავისი ეფექტური პოტენციალით, ხოლო მრავალელექტრონიანი სისტემის
ტალღური ფუნქციას ექნება ერთელექტრონიანი ტალღური ფუნქციების ნამრავლის სახე. ატომის ტალღური ფუნქციის სწორად ასაგებად აუცილებელია გავითვალისწინოთ მიკროსამყაროს ფუნდამენტური პრინციპი – ერთი ბუნების ნაწილაკთა განურჩევლობა, ანუ იგივურობა. ნაწილაკთა იგივურობის გათვალისწინებას მივყავართ ტალღური ფუნქციების გარკვეულ სიმეტრიასთან ნაწილაკთა გადასმის
მიმართ. ასე მაგალითად, ნახევრის ტოლი სპინის მქონე ნაწილაკთა (როგორებიც არიან ელექტრონები) ტალღური ფუნქციები ნიშანს იცვლიან ორი ელექტრონის გადასმისას. ამას კი თავის მხრივ მივყავართ თვისობრივად ახალ ცნებამდე როგორიც არის მაგალითად გაცვლითი ენერგია, ან გაცვლითი ურთიერთქმედება, რომელთაც ანალოგი არ გააცნიათ კლასიკურ ფიზიკაში. არაელექტროსტატიკური ბუნების ურთიერთქმედებებიდან ყველაზე მნიშვნელოვანია ელექტონის საკუთარი მაგნიტური მომენტის ურთიერთქმედება მაგნიტურ ველთან, რომელის წარმოიშობა ელექტრონის მოძრაობისას ბირთვის ველში, ანუ სპინ-ორბიტალური ურთიერთქმედება. ამ ურთიერთქმედებას გააჩნია რელატივისტური ბუნება.
სპინ-ორბიტალური ურთიერთქმედების სიმცირე საშუალებას გვაძლევს ტალღური ფუნქცია წარმოვადგინოთ ორი ფუნქციის ნამრავლის სახით, სადაც ერთი ფუნქცია დამოკიდებულია მხოლოდ სპინურ, ხოლო მეორე მხოლოდ სივრცულ ცვლადებზე. იმისათვის რომ მთლიანი ტალღური ფუნქცია იყოს ანტისიმეტრიული, სივრცული ტალღური ფუნქცია უნდა იყოს სიმეტრიული, ხოლო სპინური
ანტისიმეტრიული, ან პირიქით ნებისმიერი ორი ელექტრონის ცვლადების გადასმის მიმართ.
მრავალელექტრონიანი ატომები
მრავალელექტრონიანი ატომის ტალღური ფუნქცია აიგება ერთელექტრონიანი ტალღური ფუნქციებით ისე, რომ აგებული ფუნქცია იყოს ანტისიმეტრიული ნებისმიერი ორი ელექტრონის კოორდინატების გადასმის მიმართ. ერთელექტრონიანი ამოცანის ამოსახსნელად შემოყავთ სფერული სიმეტრიის მქონე ეფექტური პოტენციალი, რომელიც ცხადია არ არის კულონური ტიპის თუნდაც იმიტომ, რომ ელექტრონები ახდენენ ბირთვის მუხტის ეკრანირებას. ამ შემთხვევაში კულონური ველისთვის დამახასიათებელი გადაგვარება ორბიტალური მომენტით იხსნება და ერთელექტრონიანი დონეები დამოკიდებული იქნება ორ კვანტურ რიცხვზე n -ზე და l -ზე (სფერული სიმეტრიის ველში ml -ით გადაგვარება ბუნებრივია რჩება).
ატომის ერთელექტრონიანი მდგომარეობების შევსება ელექტრონებით ხდება პაულის პრინციპის დაცვით, რომლის მიხედვით ერთელექტრონიან მდგომარეობაში რომელიც ხასიათდება ოთხი კვანტური რიცხვით n , l , ml და ms შეიძლება მოთავსდეს მხოლოდ ერთი ელექტრონი. ელექრონების განაწილებას n და l კვანტური რიცხების მიხედვით უწოდებენ ელექტრონულ კონფიგურაციას და ის აღინიშნება ასე k nl სადაც k არის აღნიშნულ მდგომარეობაში მყოფი ელექტრონების რიცხვი. ექვივალენტური ელექტრონების ( n და l ერთნაირია) კონფიგურაცია შეიცავს არა უმეტეს 2(2 1) l ელექტრონს, რომელთაც აქვთ განსხვავებული ორბიტალური მომენტის გეგმილები ( 2 1 l მნიშვნელობა) და სპინის ორი პროექცია. ინდივიდუალური ორბიტალური და სპინური მომენტები ზოგადად არ
წარმოადგენენ მოძრაობის ინტეგრალებს. მოძრაობის ინტეგრალია ატომის სრული იმპულსის მომენტის მნიშვნელობა. უმეტეს შემთხვევაში ატომში რეალიზდება ე. წ. LS ბმა, რომლის დროსაც ატომის სრული იმპულსის მომენტი წარმოადგენს ატომის სრული ორბიტალური L და სრული სპინური S მომენტების ჯამს. თავის მხივ L და S მიიღება ელექტრონების ინდივიდუალური ორბიტალური მომენტების და სპინების აჯამვით. ექვივალენტური ელექტრონების მომენტების აჯამვისას L -ის და S -ის ზოგიერთი მნიშვნელობა შეიძლება შეუთავსებელი აღმოჩნდეს პაულის პრინციპთან. ამიტომ ასეთი მნიშვნელობები გამოირიცხება.
ორატომიანი მოლეკულები
მოლეკულა უფრო რთული სისტემაა ვიდრე ატომი. სირთულე ძირითადად განპირობებულია იმით, რომ ბირთვების მიერ შექმნილი ელექტრული ველი რომელშიც მოძრაობენ ელექტრონები არ არის სფერული სიმეტრიის, როგორც ეს იყო ატომებში. გარდა ამისა ბირთვებიც მოძრაობენ, რასაც ელექტრონების მოძრაობის გათვალისწინებით მივყავართ ისეთ მათემატიკურ სიძნელეებთან, რომელთა
გადაჭრა ზოგად შემთხვევაში შესაძლებელია მხოლოდ მიახლოებითი მეთოდებით.
მასათა დიდი განსხვავების გამო ბირთვები და ელექტრონები წარმოადგენენ ერთმანეთთან სუსტად დაკავშირებულ ორ ქვესისტემას – მძიმეს და მსუბუქს. ელექტრონებთან შედარებით ბირთვები მოძრაობენ იმდენად ნელა, რომ პირველ მიახლოებაში ისინი შეგვიძლია განვიხილოთ როგორც უძრავი ნაწილაკები. პიველად ეს მიახლოება განხილული იყო ბორნისა და ოპენჰაიმერის მიერ ბირთვული და
ელექტრონული ცვლადების განსაცალკევებლად მოლეკულის აღმწერ შრედინგერის განტოლებაში. ამისათვის მათ გამოიყენეს შეშფოთების თეორია, სადაც მცირე პარამეტრი იყო.
ამონარდი ატომურ ნაწილაკთა დაჯახების თეორიიდან
