ფარდობითობის ზოგადი თეორიის ელემენტები

ფარდობითობის სპეციალური თეორიის წარმოშობა განაპირობა იმ სიღრმისეულმა პრობლემებმა, რომლებიც XIX საუკუნის 60-იან წლებში ჩამოყალიბებულმა ელექტრომაგნიტური ველის მაქველის თეორიამ წამოჭრა. პრობლემატიკის გადაწყვეტაში სხვადასხვა მეცნიერმა შეიტანა ფუძემდებელი წვლილი. უპირველესად უნდა დავასახელოთ მეცნიერები ლორენცი და პუანკარე, მაგრამ ფიზიკურად დასრულებული და განსხვავებული გადაჭრა აინშტაინს ეკუთვნის-ფარდობითობის სპეციალური თეორია(1905 წ.). სპეციალური თეორიის აინშტაინისეული განზოგადების არც ექსპერიმენტული, არც თეორიული მინიშნება არ არსებობდა. ფარდობითობის ზოგად თეორიაზე მუშაობას აინშტაინი 1907 წლიდან შეუდგა, ძირითადი რელატივისური ეფექტები 1911 წელს დაადგინა, ხოლო დასრულებული სახე 1916 წელს მისცა.

ფარდობითობის ზოგადი თეორია არის გამრუდებული სივრცე-დროის, გრავიტაციის “გეომეტრიზაციის” დახვეწილი და ლამაზი, მაგრამ მეტად რთული მათემატიკური ენის ფიზიკური თეორია. შევეცადოთ გადმოვცეთ მისი არსის მოკლე მონახაზი.

ფარდობითობის სპეციალური თეორია არ ეხება ნიუტონის გრავიტაციის შორსქმდების თეორიას, რომელიც არ ეთანხმება ფარდობითობის პრინციპსა და ურთიერთქმედების გადაცემის სიჩქარის სასრულობას. მართლაც ნიუტონის მსოფლიო მიზიდულობის კანონი:

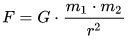
ფარდობითობის სპეციალურმა თეორიამ ფარდობითობის პრინციპი ფიზიკის უზოგადეს დებულებად, ფიზიკის საფუძვლად დაამკვიდრა. მაგრამ ფარდობითობის პრინციპი ათვლის სისტემათა სიმრავლიდან ინერციულ ათვლის სისტემებს გამოარჩევს. აინშტაინი სვმას კითხვას: რა არის ასეთი უპირატესობის ობიექტური მიზეზები? მისი პასუხია: ჩვენ არ შეგვიძლია ასეთი ობიექტური მიზეზების მოძიება. ამიტომ პრობლემას შემდეგნაირად აყენებს: განვაზოგადოთ ფარდობითობის პრინციპი არაინერციულ, ე.ი. ინერციულის მიმართ აჩქარებულად მოძრავ, ათვლის სისტემებზე-ფაქტობრივად, ნებისმიერ ათვლის სისტემაზე. მაგრამ როგორ მოვახერხოთ ეს, როდესაც ერთმანეთის ტოლფასი ინერციული ათვლის სისტემები ძირეულად განსხვავდება არაინერციული სისტემებისგან? რა ვუყოთ ინერციის პრინციპს? რა კავშირი აქვს გრავიტაციასთან ასეთ განზოგადებას? აინშტაინმა აჩვენა რომ განზოგადებისათვის ამოსავალი უნდა იყოს ინერტული და გრავიტაციული მასების ტოლობა.

ინერტული მასა იმპულსის მუდმივობის კანონის საფუძველზე განვსაზღვრავთ. მასის განსაზღვრა მსოფლიო მიზიდულობის კანონიდანაც შეიძლება. ასე განსაზღვრული მასა-გრავიტაციული მასა-გრავიტაციული ურთიერთქმედების ზომა არის. მაგალითად, სიმძმის ძალა. გრავიტაციული მასის ერთეულზე მოქმედი ძალა(მსგავსად ელექტრული ველის დაძაბულობისა), ემთხვევა თავისუფალი ვარდნის აჩქარებას. ჯერ კიდევ გალილეომ დაადგინა, რომ ყველა სხეული, მიუხედავად სხვასხვაგვარობისა, ერთნაირი აჩქარებით ვარდება a=g. მაგრამ ცდების სიზუსტე დიდი არ იყო. მასის ცნება ნიუტონმა შემოიტანა და მან უფრო ზუსტი ცდები ჩაატარა ინერტული და გრავიტაციული მასების ტოლობის შესამოწმებლად. 1894 წელს ეტვეშმა ინერტული და გრავიტაციული მასების ტოლობა 10^-9 სიზუსტით დაადასტურა. ასე რომ, აინშტაინის დროს საკმაოდ ზუსტი მონაცემები არსებობდა. ფარდობითობის ზოგადი თეორიის შექმნის შემდეგ, პრინციპული მნიშვნელობის გამო, გაზომვის სიზუსტის გაზრდა აუცილებელი გახდა. თანამედროვე მონაცემებით ინერტული და გრავიტაციული მასები 10^-12 სიზუსტითაა ტოლი. ნიუტონის ფიზიკაში მათი ტოლობა გარკვეულწილად შემთხვევით თანხვედრად აღიქმება, ვინაიდან გაურკვეველი რჩება მათი ჭეშმარიტი ბუნება. ფარდობითობის ზოგადმა თეორიამ თანხვედრას პრინციპული მნიშვნელობა მიანიჭა.

განვიხილოთ არაინერციული ათვლის სისტემები, რომელიც ინერციულის მიმართ a in მუდმივი სიჩქარით მოძრაობს. სხვადასხვა მასის თავისუფალი სხეულები ამ არაინერციული სისტემის მიმართ ყველა -a in ერთნაირი აჩქარებით-თანაბარაჩქარებულად იმოძრავებს, ე.ი. აჩქარება სხეულის მასაზე არ არის დამოკიდებული ისევე, როგორც გრავიტაციულ ველში. შევადაროთ არაინერციული სისტემა ინერციულ სისტემას, რომელშიც g დაძაბულობის ერთგვაროვანი და მუდმივი გრავიტაციული ველი გვაქვს. ასეთ ინერციულ სისტემაში ყველა სხეული g ერთნაირი აჩქარებით, თანაბარაჩქარებულად ვარდება-აჩქარება სხეულის მასაზე არ არის დამოკიდებული. მოძრაობა ორივე სისტემაში ეთნაირად მიმდენარეობს, არაინერციული სისტემა გრავიტაციული ველის გარეშე ეკვივალენტურია ინერციული სისტემისა გრავიტაციული ველით და ეს იმიტომ, რიმ გრავიტაციული და ინერტული მასები ტოლია. დავრწმუნდეთ, რომ ეკვივალენტობის შებრუნება შეიძლება: ინერციული სისტემა ერთგვაროვანი და მუდმივი გრავიტაციული ველით ტოლფასია არაინერციული ათვლის სისტემისა გრავიტაციული ველის გარეშე. ვთქვათ, ინერციული ათვლის სისტემის გრავიტაციულ ველში თავისუფლად ვარდება “აინშტაინის ლიფტი”-არაინერციული ათვლის სისტემა: ლიფტის მიმართ სხეული (რომელიც ინერციულ სისტემაში ლიფტთან ერთად ვარდება) ან უძრავი იქნება, ან თანაბარწრფივად იმოძრავებს, თუ სიჩქარეს მივანიჭებთ. მაშასადამე, შეგვიძლია ვთქვათ, რომ სხეული თავისუფალია, მასზე არაფერი მოქმედებს და თავისუფლად ვარდნილ არაინერციულ სისტემაში გრავიტაციული ველი არა გვაქვს, “გამოირთო”. ყოველთვის თუ შეიძლება ასეთი ურთიერთეკვივალენტური სისტემების შერჩევა, გრავიტაციული ველის მოსპობა? არა, რადგან გრავიტაციული ველი, საზოგადოდ, არც ერთგვაროვანია და არც მუდმივი. მაგრამ ყოველთვის შეიძლება შევარჩიოთ სივრცის იმდენად მცირე არე და დროის იმდენად მცირე შუალდები, ანუ როგორც ამბობენ, სივრცე-დროის მცირე არე, რომ გრავიტაციული ველი მის ფარგლებში მუდმივად და ერთგვაროვნად ჩავთვალოთ. ასეთ შემთხვევაშიი ყოველთვის შეიძლება ისეთი არაინერციული ათვლის სისტემის შერჩევა, რომ გრავიტაციული ველი “გამოვრთოთ”და ეს ინერტული და გრავიტაციული მასების ტოლობითაა განპირობებული. ჩამოვაყალიბოთ ფიზიკის ფუნდამენტური დებულება- ეკვივალენტობის პრინციპი, რომელიც აინშტაინმა საფუძვლად დაუდო ფარდობითობის ზოგად თეორიას:

სივრცე-დროის საკმარისად მცირე არეში არაინერციული სისტემა გრავიტაციული ველის გარეშე და ინერციული სისტემა გრავიტაციული ველით სრულიად ეკვივალენტურია: ფიზიკის ყველა კანონს ორივე სისტემაში ერთნაირი სახე აქვს.

რატომ არის ეკვივალენტობის პრონციპი ფარდობითობის პრინციპის განზოგადება არაინერციულ სისტემებზე? ფარდობითობის პრინციპის თანახმად, ყველა ინერციული ათვლის სისტემა ეკვივალენტურია: ლოკალური ფიზიკური ცდებით სისტემის შიგნით-კვლავ გავიხსენოთ გალილეის გემის ტრიუმი-შეუძლებელია სისტემის თანაბარწრფივი მოძრაობის სიჩქარის გაზომვა. ეკვივალენტობის პრინციპის თანახმად, ლოკალური ფიზიკური ცდებით შეუძლებელია ათვლის სისტემის აჩქარების გაზომვა და იმის დადგენა, რომ ათვლის სისტემა არაინერციულია გრავიტაციული ველის გარეშე, თუ ინერციულია გრავიტაციული ველით. აჩქარებული მოძრაობაც ფარდობითია, მსგავსად თანაბარწრფივი მოძრაობისა. ამით გამოიხატება ფარდობითობის პრინციპის განზოგადება არაინერციულ სისტემებზე.

ახლა აინშტაინის კითხვა დავსვათ: რა ევრისტიკული, შემეცნებითი ღირებულება აქვს ეკვივალენტობის პრინციპს, ფარდობითობის სპეციალური თეორიის განზოგადებას მის საფუძველზე? ფარდობითობის სპეციალურ თეორიაში ცნობილია ფიზიკის კანონები ინერციული ათვლის სისტემების მიმართ, როდესაც გრავიტაციული ველი არა გვაქვს, ხოლო გრავიტაციული ველის კანონები უცნობია. ინერციული სისტემიდან არაინერციულ სისტემაზე გადასვლისას ფიზიკის კანონების სახის დადგენა შესაძლებელია კოორდინატებითა და დროის გარდაქმნით(ფიზიკის ელემენტარულ კურსში არაინერციული ათვლის სისტემები არ შეისწავლება და თქმულს უფრო გასაგებს გახდის ქვემოთ გამორჩეული მაგალითი). ეკვივალენტობის პრინციპის თანახმად, ასეთი გადაყვანით გრავიტაციული ველის კანონებს მივიღებთ ინერციული სისტემის მიმართ.

როგორ ხდება მოძრაობის, ფიზიკური მოვლენის შესწავლა ფარდობითობის ზოგად თეორიაში? რატომ არის მისი მათემატიკური ენა ასე რთული? ჯერ ათვლის სისტემის თაობაზე-მისი გაგება იცვლება.

ნიუტონის ფიზიკაში ათვლის სისტემა მყარია, რომელიც მთელ სივრცეზე ვრცელდება უსასრულო დროის განმავლობაში. ასეთია ჰელიოცენტრული სისტემა, რომელიც მზის სისტემას მოიცავს და უცვლელია მისი არსებობის მანძილზე, ასეთია უძრავი ვარსკვლავების სისტემა და სხვა. ნიუტონის ფიზიკაში სივრცე ევკლიდურია-მართებულია ევკლიდეს გეომეტრია. ფარდობითობის სპეციალურმა თეორიამ სივრცე და დრო ორგანულად დააკავშირა, წარმოაჩინა ერთიანი სივრცე-დროის სახით (სივრცე-დროის კონტინუუმი), რომელიც ოთხგანზომილებიანია და ფსევდოევკლიდური. ფარდობითობის სპეციალურ თეორიაში ათვლის სისტემა კვლავ მყარია, უსაზღვროდ განფენილი მთელ სივრცე-დროში. ფარდობითობის ზოგად თეორიაში, როგორც ეკვივალენტობის პრინციპიდან ჩანს, ათლის სისტემა მხოლოდ ლოკალურია: იგი მოიცავს სივრცე-დროის საკმარისად მცირე არეს, რომლის ფარგლებშიც გრავიტაციული ველი ერთგვაროვანი და მუდმივია. ამგვარად, ფარდობითობის ზოგად თეორიაში ფიზიკური მოვლენის აღწერა და შესწავლა ლოკალურად ხდება. როგორ დავადგინოთ, არჩეული ათვლის სისტემა ლოკალურია თუ არა? ისევე როგორც ინერციული ათვლის სისტემების არჩევისას, ამ შემთხვევაშიც პასუხი დამოკიდებულია გაზომვის სიზუტეზე. სანიმუშოდ გავნიხილოთ დედამიწის ხელოვნური თანამგზავრი, როგორც ათვლის სისტემა , რომელშიც დედამიწის გრავიტაციული ველი “გამორთულია”. მასში სხეული ისე იქცევა, როგორც თავისუფალი. ავიღოთ ორი პატარა სხეული, რომლებიც უძრავია. თუ გაზომვის მოცემული სიზუსტისათვის ვერ აღმოვაჩენთ მათ ფარდობით გადაადგილებას ან აჩქარებას(რეალურად ასეც არის), თანამგზავრი ლოკალურ ათვლის სისტემად ჩაითვლება, თუ არადა-უფრო მცირე ათვლის სისტემა უნდა ავირჩიოთ.

როგორია სივრცე-დროის ლოკალური თვისებები ფარდობითობის ზოგადი თეორიის თანახმად? განვიხილოთ აინშტაინისეული მაგალითი. ვთქვათ, დისკო S ინერციული სისტემის მიმართ ბრუნავს თავისი სიბრტყის მართობი სიმეტრიის ღერძის გარშემო. დისკოს ხისტად დავუკავშიროთ S 1 სისტემა, რომელიც მასთან ერთად ბრუნავს S-ის მიმართ და ნათელია არაინერციულია, S 1-ის მიმართ ფიზიკის კანონები უცნობი, მაგრამ ვიცით ფარდობითობის სპეციალური თეორიის კანონები S-ის მიმართ და ამიტომ შეგვიძლია მათი განსაზღვრა S 1-ის მიმართაც. ამისთვის საკმარისია განვიხილოთ დროის იმდენად მცირე შუალდები და დისკოს იმდენად მცირე ელემენტი, რომ მისი ბრუნვითი მოძრაობა თანაბარწრფივად ჩავთვალოთ. გავზომოთ დისკოს შემომსაზღვრელი წრეწირისა და დიამეტრის სიგრძე,დავუშვათ გვაქვს ბევრი ზუსტად ერთნაირი პატარა მყარი ღერო, ერთეული სიგრძისა. ერთმანეთის მოყოლებით დავალაგოთ ისინი ერთ-ერთი დიამეტრისა და წრეწირის გასწვრივ. S სისტემაში ერთდროულად გავზომოთ ყველა ღეროს ბოლოთა მდებარეობა. უძრავი დისკოსათვის ცხადია, მივიღებთ რომ l/d=π. მაგრამ ბრუნვისას ასე არ იქნება. S დამკვირვლებლის თვალსაზრისით, დიამეტრზე მოთავსებულ ღეროთა სიგრძეზე მოძრაობა გავლენას არ ახდენს, რადგან სიჩქარე მართობია ღეროს (განივი ზომის ინვარიანტობა), ხოლო წრეწირის სიგრძეზე განლაგებული ღეროებუ შემოკლებულია (ლორენცის შემოკლება) – ყოველი პატარა ღერო დისკოს წრფივი სიჩქარის გასწვრივ მოძრაობს. ამიტომ წრეწირის სიგრძე მეტი გამოვა. მბრინავ ათვლის სისტემაში არ არის მართებული ევკლიდეს გეომეტრია. შემდეგ: მოვათავსოთ S სისტემის საათებიან სინქრონიზებული საათები დისკოს ცენტრსა და კიდეზე. ცენტრში მოთავსებული საათი კი მოძრაობის გამო ჩამორჩება(დროის შენელება). ჩამორჩენა დამოკიდებულია საათის მდებარეობაზე, რადგან დისკოს წრფივი სიჩქარე სხვადასხვა ადგილზე სხვადასხვაა, ე.ი. არ დრო არის ერთგვაროვანი არაინერციულ სისტემაში. ეკვივალენტობის პრინციპის თანახმად, ბრუნავი არაინერციული სისტემა ტოლფასია ინერციული სისტემისა გრავიტაციული ველით. დასკვნა: გრავიტაციული ველი სივრცე-დროის თვისებებზე მოქმდებს, სივრცე-დრო არ არის ევკლიდური(ფსევდოევკლიდური).

წმინდა მათემატიკური თვალსაზრისით, არაევკლიდური სივრცე სხვადასხვანაირი შეიძლება იყოს. ფარდობითობის ზოგადი თეორიის თანახმად, ფიზიკური დრო-სივრცე ოთხგანზომილებიანია და გამრუდებული, რომლის სიმრუდე წერტილიდან წერტილამდე იცვლება(რიმანის სივრცე). ოთხგანზომილებიანი გამრუდებული სივრცის თვალსაჩინო წარმოდგენა შეუძლებელია, იგი მხოლოდ მათემატიკურად აღიწერება. შესატყვისი საკამოდ რთული მათემატკური ენა ტენზორული აღრიცხვაა. რა იწვევს სივრცე-დროის გამრუდებას? ფარდობითობის ზოგად თეორიამდე ფიზიკური მოვლენები, მატერიის მოძრაობა განიხილებოდა სივრცე-დროის კონტინიუმში, რომლის თვისებები განსაზღვრავს მატერიის თვისებებს, მაგრამ თავად არ არის დამოკიდებული ამ უკანასკნელის თვისებებზე. აინშტაინი ხაზს უსვამს, რომ ასეთი მდგომარეობა ეწინააღმდეგება მეცნიერებისათვის დამახასიათებელ აზროვნების მეთოდს. ფარდობითობის ზოგადი თეორია წინ გადადგმული ნაბიჯია: მატერია მოქმედებს სივრცე-დროის თვისებებზე, ამრუდებს მას, ისინი ურთიერთკავშირშია.

იმის გასაგებად, თუ როგორ აიხსნება გრავიტაცია სივრცე-დროის გამრუდებით, თვალსაჩინო ორგანზომილებიანი ანალოგია მოვიშველიოთ: წარმოვიდგინოთ გაჭიმული ბატუტი, რომლის სიბრტყე ანალოგი იყოს ევკლიდური სივრცისა. ორივე შემთხვევაში მართებულია ევკლიდეს გეომეტრია, მაგალითად ბატუტი ისეა მოქსოვილი, რომ პატარა უჯრედებისგან შედგება და თითოეული უჯრედის დიაგონალისათვის პითაგორას თეორემა სრულდება. მოვათავსოთ ბატუტის შუაში მძიმე ბირთვი. ბატუტი ჩაიღუნება, უჯრედების სიბრტყე სხვასხვაგვარად გამრუდდება და მათვის აღარ იქნება მართებული პითაგორას თეორემა. მსგავსადვე სხვადასხვაგვარად გამურდდება სივრცე-დრო ნივთიერების(მატერიის) მოქმდებით-იგი აღარ იქნება ევკლიდური(ფსევდოევკლიდური). ახლა ბატუტის კიდეებთან განსხვავებული მასის პატარა ბირთვები დავაწყოთ. ისინი ჩაღუნულ ბატუტზე დაგორდებიან მძიმე ბირთვისკენ, თითქოს იგი მათ “იზიდავდეს”. ასე გამოვლინდა ბატუტის ჩაღუნვა. მიზიდვა ბატუტის ჩაღუნვით , სიმრუდით განისაზღვრება და ბირთვების მასაზე არ არის დამოკიდებული. ანალოგიურად აიხსნება გრავიტაცია, როგორც გამრუდებული სივრცე-დროის სტრუქტურის გამოვლენა, გრავიტაციული ველი “გეომეტრიული” ველია. ინერტული და გრავიტაციული მასები ერთი ბუნებისაა და ერთმანეთს ემთხვევა.

ფარდობითობის ზოგად თეორიაში მოძრაობის აღწერა ლოკალურია: მაგალითად თანამგზავრში არ იგრძნობა გრავიტაცია, ამიტომ ნუღარც ვილაპარაკებთ მასზე-სხეულები თანამგზავრში და თვით თანამგზავრი სივრცე-დროის(ლოკალურ) არეში თავისუფლად, ყოველგვარი ძალების მოქმდების გარეშე მოძრაობს “იდეალურ წრფეზე”, რომელსაც გეოდეზიურ წირს უწოდებენ. გეოდეზიური წირი არის ავკლიდეს გეომეტრიის წრფის განზოგადება ოთხგანზომილებიანი გამრუდებული სივრცე-დროისთვის, ხოლო თავისუფალი მოძრაობა გამრუდებული სივრცე-დროის ლოკალურ არეში-ინერციის პრინციპისა. გეოდეზიურ წირზე მოძრაობს გასროლილი ქვა, პლანეტები მზის გარშემო.. ლოკალური სიმრუდეები იკარგება, რომლებიც ამ შემთხვევაში მცირეა და დიდ მანძილებზე გრავიტაციული მიზიდვის ეფექტს გვაძლევს, რაც კარგად აღიწერება ნიუტონისეული მსოფლიო მიზიდულობის ფენომენოლოგიური (“ფიქტიურ”) ძალით.

ავტორი: თამაზ ხაზარაძე