აზრობრივი ექსპერიმენტი

ეს ცნება პირველად შემოიტანა გალილეო გალილეიმ.
მაგალითები:

✨ დახრილი სიბტყეზე ჩამოსრიალების შემდეგ სხეული ჩერდება ხახუნის გამო. ამიტომ ხახუნს თუ შევამცირებთ სხეული კიდევ უფრო შორს გაჩერდება და ზღვარში თუ გამოვრიცხავთ ხახუნს ის არ უნდა გაჩერდეს. მაგრამ ასეთი ცდის ჩატარება რეალურად შეუძლებელია, რადგანაც ხახუნს ვერ გამოვრიცხავთ და მხოლოდ აზრობრივად შეგვიძლია ‘’ჩავატაროთ’’ ეს ცდა ანუ ვთვათ, რომ სხეული არ გაჩერდება თუ ხახუნი არ არის.

✨ საქანი ხახუნის გამო ჩერდება. ამიტომ აზრობრივი ექსპერიმენტი იქნება: თუ ხახუნს გამოვრიცხავთ საქანი არ გაჩერდება და სწორედ ამ შემთხვევისთვია არის დაწერილი მათემატიკური საქანის პერიოდის ფორმულა:

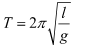
შემდეგ ეს ცნება განაზოგადა ალბერტ აინშტაინმა ფარდობითობის თეორიაში. ტუპების პარადოქსი- ერთი ტყუპისცალი დედამიწაზე რჩება და მეორე მიემგზავრება ხანგრძლივ კოსმოსურ მოგზაურობაში სუბსინათლის სიჩქარით, მისი დაბრუნების შემდეგ აღმოჩნდება, რომ დედამიწაზე დარჩენილი ტყუპისცალი უფრო ასაკოვანია, ხოლო ის ვინც გაემგზავრა ახალგაზრდა, რადგან დედამიწაზე მყოფი დამკვირვებლისათვის დრო კოსმოსურ ხომალდში უფრო ნელა მიდის მისი წარმოუდგენელი სიჩქარის გამო. ამ ფაქტის პარადოქსულობა იმაში მდგომარეობს, რომ იგივე დასკვნა შეუძლია გამოიტანოს მეორე, მოგზაურობაში წასულმაც.

აინშტაინის მიერ სპეციალური ფარდობითობის თეორიის შექმნას მაშინვე მოჰყვა უამრავი უჩვეულო მოვლენის წინასწარმეტყველება და ერთი შეხედვით პარადოქსული ამოცანები, რომელთა შორის ტყუპების პარადოქსი ყველაზე ადვილად გასაგები და პოპულარული
თავსატეხია: ტყუპისცალიდან ერთ -ერთი მიემგზავრება ძალიან სწრაფი რაკეტით მეზობელი ვარსკვლავისკენ და ბრუნდება უკან. რადგან სწრაფად მოგზაური ტყუპისცალისთვის დრო შენელებულია, გამოდის, რომ ის დედამიწაზე დაბრუნებისას უფრო ახალგაზრდა უნდა იყოს ვიდრე დედამიწაზე დარჩენილი მისი ტყუპისცალი. მეორეს მხრივ კი, ფარდობითობის პრინციპის თანახმად მოგზაური ტყუპისცალის ათვლის სისტემაში დედამიწაზე დარჩენილი ტყუპი მოძრაობს, თვითონ კი უძრავია, ამიტომ მოგზაური ტყუპისცალი ფიქრობს, რომ დედამიწაზე დარჩენილი ტყუპისთვის დრო უფრო ნელა უნდა გადიოდეს და ამიტომ დედამიწაზე დაბრუნების შემდეგ დედამიწაზე დარჩენილი ტყუპი მასზე ახალგაზრდა უნდა იყოს. ესაა პარადოქსული შედეგი, მაგრამ მხოლოდ ერთი შეხედვით. სინამდვილეში მოგზაურ ტყუპისცალთან დაკავშირებული ათვლის სისტემა არ შეიძლება ინერციულად ჩაითვალოს, ამიტომაც თუ მხოლოდ ერთ ინერციულ ათვლის სისტემას გამოვიყენებთ, ის უნდა დავუკავშიროთ დედამიწაზე დარჩენილ ტყუპისცალს და დროის შენელების მექანიზმი მოგზაურ ტყუპისცალს უკავშირდება, შედეგი ცალსახაა და მოგზაური უფრო ახალგაზრდა იქნება დედამიწაზე დაბრუნების შემდეგ ვიდრე მისი დედამიწაზე დარჩენილი ტყუპისცალი.
მოგზაურ ტყუპისცალს კი ათვლის სისტემების წყვილი უნდა შევუსაბამოთ იმისთვის, რომ მის ათვლის სისტემაში გასაგები გახდეს რატომ ექნება დროითი ჩამორჩენა დედამიწაზე დატოვებულ ტყუპისცალთან შედარებით.[1]

წყარო:

https://rustaveli.org.ge/res/docs/c2a91b28469acdf0560b9e5f06a9e4b146197fe9.pdf

https://demonstrations.wolfram.com/GalileosThoughtExperimentOnInertia/