ჰორიზონტი. ასტრონომიული ობიექტებისა და მოვლენების შესწავლა-კვლევის საფიძველსა და პირველსაწყისს დაკვირვება ანუ დამზერა წარმოადგენს. ასტრონომიული მეცნიერების ჩასახვა მაშინ დაიწყო, როცა ადამიანი გარემოსა და ცას დააკვირდა.
ჩვენც გარემოს დაკვირვებით დავიწყოთ ასტრონომიის შესწავლა, ამისთვის უკეთესია გავიდეთ გაშლილ ადგილას-ტრიალ მინდორზე, რათა ხელს არ გვიშლიდეს ახალო ამართული მაღალი ნაგებობანი ან მთები, თუმცა მაღალი შენობის სახურავიც გამოგვადგება, როგორც ადგილი ამგვარი დაკვირვებისათვის.
ვთქვათ დღეა, შემოვავლოთ თვალი არე-მარეს, გავიხედოთ სადამდეც თვალი მიგვწვდება, დავაკვირდეთ გარემოს.
რას დავინახავთ? რა იქნება ის მთავარი, რასაც შევნიშნავთ? დედამიწის ზედაპირის ნაწილს, რომელსაც ჩვენ გარშემო შორ მანძილზე ვხედავთ, წრის მოყვანილობა აქვს. ყოველ მხარეს, ჩვენ ირგვლივ, ყველა მიმართულებით დედამიწის ზედაპირი ერთნაირად შორსაა გაჭიმული. შორს ვხედავთ თითქოს მის ნაპირს ანუ კიდეს, წრეწირივით შემოვლებულს, ამ წრეწირის შუაში ჩვენ ვიმყოფებით, უფრო ზუსტად, მის ცენტრში მოთავსებულია ჩვენი ანუ დამკვირვებლის თვალი.
ჩვენს ზემოდან გაშლილია ცა, უზარმაზარი გუმბათივით გადმოფარებული. ამ გუმბათის ანუ ნახევრსფეროს კიდეები თითქოს დედამიწის ზედაპირის შემომსსაზღვრელ წრეწირს ებჯინება, აქ თითქოს ცისა და დედამიწის მიჯნაა.
წრეწირს, სადაც თითქოს დედამიწა მთავრდება და ცა იწყება ხილულ ჰორიზონტს უწოდებენ. ეს წრეწირი ის საზღვარია, სადამდეც დამკვირვებლის თვალი წვდება დედამიწის ზედაპირს. ჰორიზონტი წრიულია იმის გამო, რომ დედამიწას სფეროს მოყვანილობა აქვს.
ცა. ცის სფერო. არც ცის საზღვარია აქ. ცა მთლიანად გარემოიცავს დედამიწას. თუმცა იგი ისე გვესურათხატება, თითქოს რაღაც ნივთიერი გუმბათიაო, სინამდვილეში უბრალოდ სივრცეა დედამიწის გარშემო. ეს სივრცე უსასრულოა. დედამიწის უშუალო მახლობლობაში იგი უკავია დედამიწის გარემომცველ ატმოსფეროს, რომელიც დღისით მოწმენდილ ცას მისთვის დამახასიათებელ მტრედისფერს ანიჭებს. ჰაერის მოლეკულებზე მზის სინათლის გაბნევის ფიზიკური კანონზომიერება განსაზღვრავს ამ ფერს. ღამით მოწმენდილი ცა ბნელია, თითქოს “შავია” და მიუხედავად ამისა, მოკიაფე ვარკვლავებით მოჭედილი ცაც ტოვებს ნახევრასფეროს შთაბეჭდილებას. ცის გუმბათს ხშირად ცის თაღს ანუ ცამრგვალს უწოდებენ. რადგნაც დედამიწის გარშემო უსასრულო სივრცეში ყველა მიმართულებით თითქმის ერთნაირ მანძილზე ვხედავთ მზეს, მთვარეს, ვარსკვლავებსა და საერთოდ ყველა მნათობს, სურათი თავისთავად ისე წარმოგვიდგება, თითქოს მნათობები ერთი სფეროს შიდა ზედაპირზე მდებარეობენ, ხოლო ჩვენ ამ სფეროს ცენტრში ვიმყოფებით. ცას აღვიქვამთ სფეროს შიდა ზედაპირს.
ნებისმიერი რადიუსის მქონე წარმოსახვით სფეროს-ცენტრით სივრცის რომელიმე წერტილში-რომლის ზედაპირზე მნათობები აღნიშნულია ისე, როგორც ისინი ცენტრიდან ჩანან დროის რომელიმე მომენტში, ეწოდება ცის სფერო.
ცის სფეროს ზედაპირამდე “მანძილი” განუსაზღვრელია და არ გამოიხატება სიგრძის ერთეულის გარკვეული რიცხვით. ამიტომ ცის სფეროს რადიუსი შეგვიძლია ჩავთვალოთ 1-ის ტოლად. მაშასადამე ცას განვიხილავთ, როგორც ერთეულიანი რადიუსის მქონე სფეროს. ასეთი წარმოდგენა გაგვიადილებს როგორც მოვლენების გეომეტრიულ ინტერპრეტაციას, ისე გამოთვლებს.
ჰორიზონტის სიშორე. კვლავ ჰორიზონტს დავაკვირდეთ. თუ მინდორში დედამიწის ნიადაგზე ვდგავართ, ჩვენი თვალთახედვის არე დიდი არაა, ჩვენი ჰორიზონტის სიშორე 4-5 კმ-ია. ე.ი. ამ მანძილებამდე ვხედავთ ჩვენ გარშემო ყოველი მიმართულებით, ტრიალ მინდორში ან შუა ზღვაში. თუ ახლა, რაიმე ამაღლებულ ადგილზე ავალთ, მაგალითად მაღალი ნაგებობების თავზე, ან ტრიალ მინდორში ამართულ ბორცვზე, დედამიწის ზედაპირი, მისი სიმრუდის გამო, უფრო შორს დაინახება. ჩვენი დაკვირვების ჰორიზონტი გაფართოვდება. ჰორიზონტის სიშორე მოიმატებს.
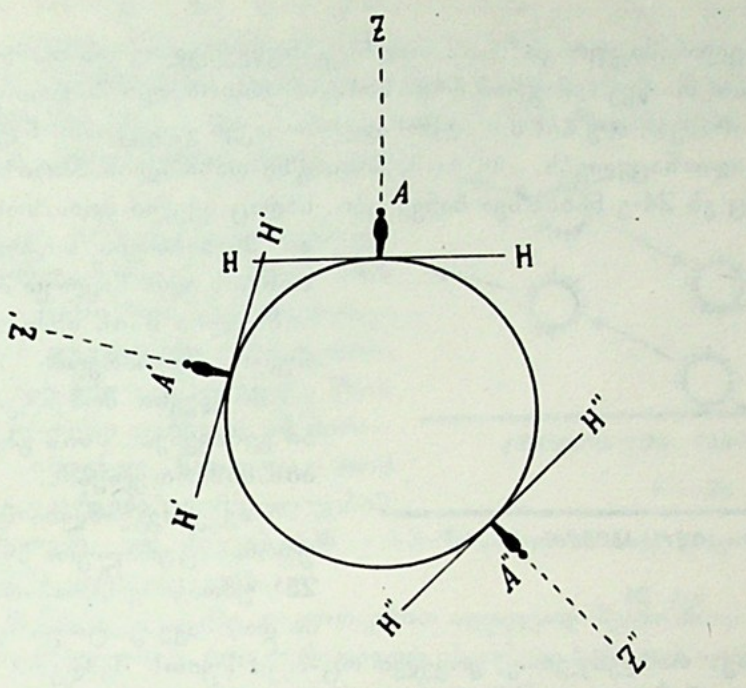
ზენიტი. ჭეშმარიტი ჰორიზონტის მართობული მიმართულება შვეული ანუ ვერტიკალური მიმართულებაა. დამკვირვებლის ადგილიდან (თვალიდან) გავლებული ვერტიკალური მიმართულების გადაკვეთა ცის სფეროსთან გვაძლევს Z წერტილს, რომელსაც ზენიტის წერტილი ან უბრალოდ ზენიტი ეწოდება. ზენიტი პირდაპირ დამკვირვებლის თავს ზემოთ არის მოთავსებული.

თუ ZA მიმართულებას ქვევით გაგრძელებულად წარმოვიდგნეთ, მისი გადაკვეთით ცის სფეროსთან მივიღებთ წერტილს, რომელსაც ნადირის წერტილი ეწოდება. ის რაც ჩვენთვის ნადირის წერტილია, ჩვენი ანტიპოდისთვის ზენიტს წარმოადგენს. ჩვენი ზენიტი კი ჩვენივე ანტიპოდის ნადირის წერტილია.

ცხადია, რომ ზენიტი სხვადასხვა დამკვირვებლისათვის სხვადასხვა წერტილშია მოთავსებული. ასევე ყოველ დამკვორვებელს თავისი ჰორიზონტი შეესაბამება.
ავტორი: ევგენი ხარაძე
1991 წელი
