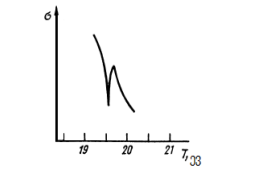
ელექტრონების ატომებზე დრეკადი გაბნევის სისტემატური ექსპერიმენტული შესწავლა დაიწყო გასული საუკუნის 20-იან წლებში რამზაუერის მიერ და უკვე მომდევნო ათწლეულში დადგენილი იქნა განივკვეთის ყოფაქცევის ძირითადი კანონზომიერებები. ნახაზზე 9 ნაჩვენებია ელექტრონების დრეკადი გაფანტვის სრული განივკვთები ზოგიერთ ატომთა ჯგუფზე, რომლებიც მკვეთრად განსხვავდებიან ერთმანეთისაგან ელექტრონული სტრუქტურით.
ჩამოვთვალოთ განსაკუთრებით დამახასიათებელი თავისებურებები, რომლებიც ჩანს ნახაზზე:
- გაფანტვის განივკვეთები დამოკიდებულია დამჯახებელი ელექტრონის
ენერგიაზე არამონოტონურად; - Ar, Kr, Xe-ის ატომებზე გაფანტვის განივკვეთს გააჩნია მინიმუმი დამჯახებელი
ელექტრონის მცირე სიჩქარეებზე (რამზაუერ-ტაუნსენდის ეფექტი) ; - ქიმიურად მსგავსი ელემენტების განივკვეთის მრუდები მსგავსია;
- ინერტული გაზის ატომებიდან ტუტე ელემენტთა ატომებზე გადასვლისას
განივკვეთი ერთი-ორი რიგით იზრდება.
ჩამოთვლილი თავისებურებების უკვე პირველი პუნქტები ეწინააღმდეგება კლასიკურ წარმოდგენებს, რომელთა მიხედვით სიჩქარის გაზრდასთან ერთად დრეკადი გაფანტვის განივკვეთი მინოტონურად უნდა ეცემოდეს. აღსანიშნავია ის ფაქტიც, რომ არამონოტონური არეები ძირითადად მცირე სიჩქარეების არეშია, ანუ იქ სადაც განსაკუთრებით უნდა გამოჩნდეს ტალღური თვისებები. ქიმიურად მსგავსი
ელემენტების განივკვეთების მსგავსება მიუთითებს იმაზე, რომ გაფანტვის პროცესში ძირითადად მონაწილეობენ სავალენტო ელექტრონები. ბუნებრივია ამ ფაქტით აიხსნება ისიც, რომ ვინაიდან ტუტე ატომების გეომეტრიული ზომები
მნიშვნელოვნად აღემატება ინერტული ატომების ზომებს, ელექტრონების ტუტე ელემენტთა ატომებზე გაფანტვის განივკვეთებიც მეტია.

ამრიგად, ელექტრონების ატომებზე დრეკადი გაფანტვის განივკვეთის ყოფაქცევის პირველადი ანალიზი მიუთითებს იმაზე, რომ განივკვეთის ენერგიაზე კლასიკური დამოკიდებულება, როგორც უნდა იყოს, თავს იჩენს შედარებით მაღალ ენერგიებზე, ხოლო „ანომალია“ კი გვაქვს მცირე ენერგიებზე. კიდევ ერთი მნიშვნელოვანი მოვლენა, რომელიც არ თავსდება კლასიკური აღწერის ჩარჩოებში არის რეზონანსები. ეს არის მკვეთრი პიკების არსებობა განივკვეთის სიჩქარეზე დამოკიდებულების მრუდზე, რომლებიც ჩნდებიან მხოლოდ მაშინ როდესაც ელექტონული ნაკადი ძალზე მონოენერგეტიკულია, ანუ როდესაც განსხვავება ელექტონის ენერგიებს შორის არ აღემატება 10-1 – 10-2 ელექტრონ-ვოლტს.
ამ ტიპის რეზონანსები შეესაბამებიან ატომის კვაზისტაციონარული მდგომარეობის შექმნას. ეს მდგომარეობა იქმნება მაშინ როდესას ატომი დაცემულ ელექტრონს ჩაიჭერს ავტოიონიზაციურ მდგომარეობაში, რომლის სიცოცხლის ხანგრძლივობა გაცილებით მეტია ელექტრონის ატომთან დაჯახების დროზე.
ყოველივე ეს გვარწმუნებს იმაში, რომ ელექტონების ატომებთად დაჯახების შესასწავლად უნდა გამოვიყენოთ კვანტურ-მექნიკური აპარატი. ამ აპარატის შესაქმნელად ჩვენ არ წავალთ ამოცანის ფორმალური და მკაცრი გადაჭრის გზით (ეს გაკეთდა კვანტური მექანიკის კურსის ფარგლებში), არამედ გამოვიყენებთ ანალოგიას კვანტურ და კლასიკურ შედეგებს შორის. ამ მიზნით ვნახოთ თუ როგორ შეიძლება
„შევასწოროთ“ დრეკადი გაბნევის კლასიკური გამოსახულება, რომ მივიღოთ მისი კვანტურ-მექანიკური ანალოგი. კვანტურ მექანიკაში ნაწილაკის მდგომარეობის დასახასიათებლად შემოდის ალბათობის ცნება, შესაბამისად მოდით განივკვეთის კლასიკურ გამოსახულებაში
შევიტანოთ სამიზნე მანძილის მქონე ნაწილაკის აღმოჩენის ალბათობის სიმკვრივე, რომელიც აღვნიშნოთ P( ) -თი.
ბრტყელი ტალღის წარმოდგენით უსასულო ტალღათა ერთობლიობით ჩვენ მნიშვნელოვნად გავართულებდით გაფანტვის ამოცანას, რომ არა შესაძლებლობა, რომ ფიზიკური მოსაზრებიდან გამომდინარე უსასრულო ჯამში შემოვიფარგლოთ წევრების მხოლოდ შედარებით მცირე რაოდენობით და ზოგჯერ შეიძლება ერთი წევრითაც კი. უფრო გასაგები რომ გავხადოთ ნათქვამი, მოდით განვიხილოთ ორი
ბილიარდის ბურთის შუბლური დაჯახება. ამ პროცესის კვანტურ-მექანიკური აღწერისას გაშლაში შეიძლება დავიტოვოთ მხოლოდ პირველი წევრი. მართლაც, თუ ძალური ველი ხასიათდება a ქმედების რადიუსით, მაშინ გაფანტვაში ძირითადი წვლილი შეაქვთ დაჯახების პარამეტრებს. დაჯახებაში ძირითადი წვლილი შეაქვთ იმ პარციალურ ტალღებს რომელთა შესაბამისი მომენტები აკმაყოფილებენ პირობას.
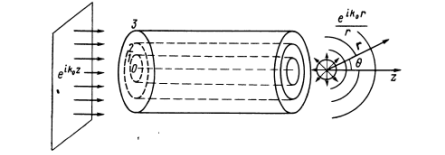
როცა ნაწილაკის სიჩქარე არ არის დიდი, ხოლო დე ბროილის ტალღის სიგრძე ბევრად აღემატება გამფანტავი არის ზომებს ან იმავე
რიგისაა, გაფანტვის ამპლიტუდაში წვლილი შეაქვს პარციალური ტალღების მცირე რაოდენობას, რაც მნიშვნელოვნად აადვილებს გაფანტვის ამოცანის ანალიზურ განხილვას.
სიჩქარის გაზრდასთან ერთად იზრდება იმ პარციალური ტალღების რიცხვი, რომლებიც უნდა გავითვალისწინოთ და შესაბამისად, პარციალური ტალღების აჯამვის ამოცანა ძალზე რთულდება. ინტუიციურად ცხადია, რომ პარციალური ტალღების დიდი რიცხვის შემთხვევაში, რომელთაც შეაქვთ წვლილი მოცემულ კუთხეზე გაფანტვის ამპლიტუდაში, ეს უკანასკნელი უნდა გადაიქცეს გარკვეულ
ინტეგრალად, რომელიც აიღება გამფანტავი პოტენციალის მოქმედების არეში. მოდით, მივიღოთ ინტეგრალური განტოლება, რომელიც შრედინგერის განტოლების ექვივალენტური იქნება და ვიპოვოთ ამ ინტეგრალური განტოლების ფორმალური ამონახსნი. შრედინგერის განტოლება ჩავწეროთ შემდეგი სახით

ელექტრონების ატომებზე არადრეკადი გაფანტვის სრული განივკვეთის მახასიათებელი დამოკიდებულება, რომელიც ზოგადია ყველა ზღურბლური პროცესისათვის მდგომარეობს იმაში, რომ ზღურბლურ ენერგიაზე ნაკლებ ელექტრონის ენერგიებზე განივკვეთი ნულის ტოლია, შემდეგ იზრდება გადის მაქსიმუმზე და მაღალ ენერგიებზე მცირდება. მაღალ ენერგიებზე განივკვეთის შემცირება გამოწვეულია დაცემული ელექტრონის სამიზნის ელექტრონებთან ურთიერთქმედების დროის შემცირებით. ატომის ელექტრონული მდგომარეობების
აგზნების მაქსიმუმი დაიმზირება დამჯახებელი ელექტრონების ისეთ სიჩქარეებზე, რომლებიც სიდიდით ატომის ბმული ელექტრონების სიჩქარეების რიგისაა.
წყარო:
ამონარიდი დაჯახების თეორიიდან
